Question

How do you find $\left| x+iy \right|$ ?

Answer 1

Hint: A modulus sign is mostly used to find the distance of an object or a point on a plane from the origin. So, to find the distance of our given expression, $\left| x+iy \right|$ we use the Pythagoras theorem. Here we consider $x,y$ as the sides of the right triangle whereas the hypotenuse of the triangle will be the distance we shall find.

Complete step by step solution:
The given expression is $\left| x+iy \right|$
The complex number is included in a modulus sign. It means that we need to find the distance of that complex number on a complex plane from the origin.
To achieve this, we use the Pythagoras theorem.
Here we consider $x,y$ as the sides of the right triangle whereas the hypotenuse of the triangle will be the distance we need to find.
The reason why finding the length of the hypotenuse is the same as the distance of that point from the origin is that the point is expressed in rectangular coordinates and the diagonals are of the same length.

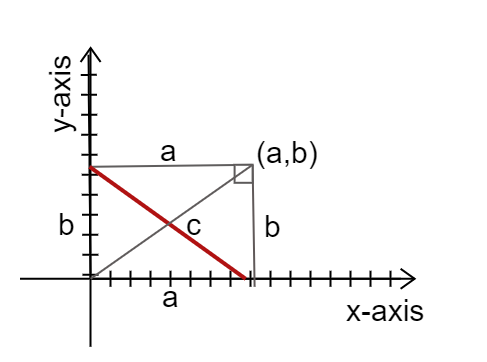
Firstly, plot the complex number, $x+iy$ on the cartesian plane. Represent it in a rectangular way so that we can find the length of the diagonal which is the distance of that point from the origin.
The complex number $z=x+iy$ can be represented on the plane as the coordinates, $\left( x,y \right)$
Given that $x$ is the real part of the complex number and $y$ is the imaginary part of the complex number.
According to the Pythagoras theorem,
In a right-angled triangle, the length of hypotenuse if given by,
$\Rightarrow c=\sqrt{{{x}^{2}}+{{y}^{2}}}$
This is also the distance from that point from the origin because the length of diagonals in a rectangle are equal.

Hence $\left| x+iy \right|$ is equal to the length $\sqrt{{{x}^{2}}+{{y}^{2}}}$.

Note: There is another way to express this notation.
Let us consider $z=x+iy$
Since $\left| x+iy \right|=\sqrt{{{x}^{2}}+{{y}^{2}}}$ ,
We can write ${{x}^{2}}+{{y}^{2}}=\left( x+iy \right)\left( x-iy \right)$
$\Rightarrow {{x}^{2}}-{{i}^{2}}{{y}^{2}}$
And since ${{i}^{2}}=-1$
$\Rightarrow {{x}^{2}}-\left( -1 \right){{y}^{2}}$
$\Rightarrow {{x}^{2}}+{{y}^{2}}$
Now, $\left| x+iy \right|=\sqrt{\left( x+iy \right)\left( x-iy \right)}$
Since $z=x+iy$ and its complement, $\bar{z}=x-iy$ .
This can be again written as,
$\Rightarrow \left| z \right|=\sqrt{z\times \bar{z}}$