
How do you factor \[{x^3} - {x^2} + x - 6 = 0\] ?
Answer
555k+ views
Hint:This question involves the arithmetic operations like addition/ subtraction/ multiplication/ division. Also, we need to know how to multiply \[x\] the term with the constant term, \[x\] a term with the\[x\] term, and the constant term with the constant term. Also, we need to know the substitution process to solve this question. The final answer would be a simplified form of the given equation.
Complete step by step solution:
The given equation is shown below,
\[{x^3} - {x^2} + x - 6 = 0 \to \left( 1 \right)\]
For solving the above equation we can assume
\[x = ... - 2, - 2,0,1,2,....\]
To find the first factor of the given equation, let’s try \[x = 1\]
\[\left( 1 \right) \to {x^3} - {x^2} + x - 6 = 0\]
\[
{\left( 1 \right)^3} - {\left( 1 \right)^2} + 1 - 6 = 0 \\
1 - 1 + 1 - 6 = 0 \\
- 5 \ne 0 \\
\]
So, \[x = 1\] is not a factor of the given equation.
Let’s try \[x = 2\]
\[\left( 1 \right) \to {x^3} - {x^2} + x - 6 = 0\]
\[
{\left( 2 \right)^3} - {\left( 2 \right)^2} + 2 - 6 = 0 \\
8 - 4 + 2 - 6 = 0 \\
8 - 8 = 0 \\
0 = 0 \\
\]
So, \[x = 2\] is a factor of the given equation.
So, the equation \[\left( 1 \right)\] can also be written as,
\[\left( 1 \right) \to {x^3} - {x^2} + x - 6 = 0\]
\[\left( {x - 2} \right)\left( ? \right) = 0 \to \left( 2 \right)\]
Here, the first factor is known, so we would find the second factor of the given equation.
From the equations \[\left( 1 \right)\] and \[\left( 2 \right)\], we get
\[{x^3} - {x^2} + x - 6 = \left( {x - 2} \right)\left( ? \right) = 0 \to \left( 3 \right)\]
First, we need to build \[{x^3}\]
So, we write
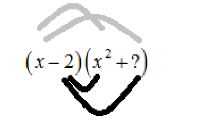
It gives \[{x^3}\]. But \[ - 2 \times {x^2}\]gives\[ - 2{x^2}\]
So, we get
\[\left( {x - 2} \right)\left( {{x^2} + ?} \right) = {x^3} - 2{x^2} + ?\]
Next, we need to build \[ - {x^2}\], already we have \[ - 2{x^2}\]. So, if we put \[{x^2}\] we get,
\[ - 2{x^2} + {x^2} = - {x^2}\]
So, we get
\[
\left( {x - 2} \right)\left( {{x^2} + x + ?} \right) = {x^3} - 2{x^2} + {x^2} - 2x + ? \\
\left( {x - 2} \right)\left( {{x^2} + x + ?} \right) = {x^3} - {x^2} - 2x + ? \\
\]
Next, we need to build\[x\]. We already have \[ - 2x\]. So, we put \[3x\]
\[ - 2x + 3x = x\]
So, we get
\[
\left( {x - 2} \right)\left( {{x^2} + x + 3 + ?} \right) = {x^3} - {x^2} - 2x + 3x - 6 \\
\left( {x - 2} \right)\left( {{x^2} + x + 3 + ?} \right) = {x^3} - {x^2} + x - 6 \\
\]
Next, we need to build \[ - 6\]. We already have \[ - 6\]
So, we get
\[\left( {x - 2} \right)\left( {{x^2} + x + 3} \right) = {x^3} - {x^2} + x - 6\]\[ \to \left( 4 \right)\]
By comparing the equation \[\left( 3 \right)\]and\[\left( 4 \right)\], we get
\[{x^3} - {x^2} + x - 6 = \left( {x - 2} \right)\left( {{x^2} + x + 3} \right)\]
So, finally, we get the second factor as,
\[\left( {{x^2} + x + 3} \right)\]
We can’t simplify the term further.
So, the final answer is,
\[{x^3} - {x^2} + x - 6 = \left( {x - 2} \right)\left( {{x^2} + x + 3} \right)\]
Note: This question involves the arithmetic operation of addition/ subtraction/ multiplication/ division. Note that for finding the first factor in these types of questions we have to assume the \[x\] values and check them with the given equation. If the\[x\]value satisfies the given equation we can take it as one of the factors of the given equation.
Complete step by step solution:
The given equation is shown below,
\[{x^3} - {x^2} + x - 6 = 0 \to \left( 1 \right)\]
For solving the above equation we can assume
\[x = ... - 2, - 2,0,1,2,....\]
To find the first factor of the given equation, let’s try \[x = 1\]
\[\left( 1 \right) \to {x^3} - {x^2} + x - 6 = 0\]
\[
{\left( 1 \right)^3} - {\left( 1 \right)^2} + 1 - 6 = 0 \\
1 - 1 + 1 - 6 = 0 \\
- 5 \ne 0 \\
\]
So, \[x = 1\] is not a factor of the given equation.
Let’s try \[x = 2\]
\[\left( 1 \right) \to {x^3} - {x^2} + x - 6 = 0\]
\[
{\left( 2 \right)^3} - {\left( 2 \right)^2} + 2 - 6 = 0 \\
8 - 4 + 2 - 6 = 0 \\
8 - 8 = 0 \\
0 = 0 \\
\]
So, \[x = 2\] is a factor of the given equation.
So, the equation \[\left( 1 \right)\] can also be written as,
\[\left( 1 \right) \to {x^3} - {x^2} + x - 6 = 0\]
\[\left( {x - 2} \right)\left( ? \right) = 0 \to \left( 2 \right)\]
Here, the first factor is known, so we would find the second factor of the given equation.
From the equations \[\left( 1 \right)\] and \[\left( 2 \right)\], we get
\[{x^3} - {x^2} + x - 6 = \left( {x - 2} \right)\left( ? \right) = 0 \to \left( 3 \right)\]
First, we need to build \[{x^3}\]
So, we write
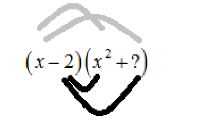
It gives \[{x^3}\]. But \[ - 2 \times {x^2}\]gives\[ - 2{x^2}\]
So, we get
\[\left( {x - 2} \right)\left( {{x^2} + ?} \right) = {x^3} - 2{x^2} + ?\]
Next, we need to build \[ - {x^2}\], already we have \[ - 2{x^2}\]. So, if we put \[{x^2}\] we get,
\[ - 2{x^2} + {x^2} = - {x^2}\]
So, we get
\[
\left( {x - 2} \right)\left( {{x^2} + x + ?} \right) = {x^3} - 2{x^2} + {x^2} - 2x + ? \\
\left( {x - 2} \right)\left( {{x^2} + x + ?} \right) = {x^3} - {x^2} - 2x + ? \\
\]
Next, we need to build\[x\]. We already have \[ - 2x\]. So, we put \[3x\]
\[ - 2x + 3x = x\]
So, we get
\[
\left( {x - 2} \right)\left( {{x^2} + x + 3 + ?} \right) = {x^3} - {x^2} - 2x + 3x - 6 \\
\left( {x - 2} \right)\left( {{x^2} + x + 3 + ?} \right) = {x^3} - {x^2} + x - 6 \\
\]
Next, we need to build \[ - 6\]. We already have \[ - 6\]
So, we get
\[\left( {x - 2} \right)\left( {{x^2} + x + 3} \right) = {x^3} - {x^2} + x - 6\]\[ \to \left( 4 \right)\]
By comparing the equation \[\left( 3 \right)\]and\[\left( 4 \right)\], we get
\[{x^3} - {x^2} + x - 6 = \left( {x - 2} \right)\left( {{x^2} + x + 3} \right)\]
So, finally, we get the second factor as,
\[\left( {{x^2} + x + 3} \right)\]
We can’t simplify the term further.
So, the final answer is,
\[{x^3} - {x^2} + x - 6 = \left( {x - 2} \right)\left( {{x^2} + x + 3} \right)\]
Note: This question involves the arithmetic operation of addition/ subtraction/ multiplication/ division. Note that for finding the first factor in these types of questions we have to assume the \[x\] values and check them with the given equation. If the\[x\]value satisfies the given equation we can take it as one of the factors of the given equation.
Recently Updated Pages
Master Class 11 Computer Science: Engaging Questions & Answers for Success

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Master Class 11 Maths: Engaging Questions & Answers for Success

Master Class 11 Biology: Engaging Questions & Answers for Success

Trending doubts
One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

There are 720 permutations of the digits 1 2 3 4 5 class 11 maths CBSE

Discuss the various forms of bacteria class 11 biology CBSE

Draw a diagram of a plant cell and label at least eight class 11 biology CBSE

State the laws of reflection of light

Explain zero factorial class 11 maths CBSE




