Question

How do you factor ${x^3} - 9{x^2} + 27x - 27$?

Answer 1

Hint:To order to determine the factors of the above cubic equation ,use of the formula of$\left( {{A^3} - {B^3}} \right) = \left( {A - B} \right)\left( {{A^2} + A.B + {B^2}} \right)$for the first and last term and pull common $ - 9x$from both left terms .We’ll get a product to linear and quadratic equation and to factorise the quadratic one use the formula \[{A^2} - 2AB + {B^2} = {(A - B)^2}\]to find all the factors .

Complete step by step solution:
Given a Cubic equation${x^3} - 9{x^2} + 27x - 27$,let it be $f(x)$
$f(x) = {x^3} - 9{x^2} + 27x - 27$

Comparing the equation with the standard cubic equation $a{x^3} + b{x^2}cx + d$
a becomes 1

b becomes -9

c becomes 27

and d becomes -27

To find the cubic factorization,

First rearranging the terms,
$
f(x) = {x^3} - 27 - 9{x^2} + 27x \\
f(x) = {x^3} - {3^3} - 9{x^2} + 27x \\
$
Now applying formula$\left( {{A^3} - {B^3}} \right) = \left( {A - B} \right)\left( {{A^2} + A.B + {B^2}}
\right)$in the first two terms taking $A\,as\,x$and $B\,as\,3$ pulling out common $ - 9x$from the last two terms
$ = (x - 3)({x^2} + 3x + 9) - 9x(x - 3)$

Taking common $(x - 3)$
$ = (x - 3)({x^2} + 3x + 9 - 9x)$

Combining all like terms
$
= (x - 3)({x^2} - 6x + 9) \\
= (x - 3)({x^2} - 2(3)(1)x + {3^2}) \\
$

The quadratic part of the expression can be factored using formula\[{A^2} - 2AB + {B^2} = {(A - B)^2}\]

Now our equation becomes
$ = (x - 3){(x - 3)^2}$
Using property of exponent${a^m} \times {a^n} = {a^{m + n}}$
$ = {(x - 3)^3}$
$f(x) = {(x - 3)^3}$
Hence, we have successfully factorized our cubic equation.

Therefore, the factors are $(x - 3)(x - 3)(x - 3) = {(x - 3)^3}$

Formula:
$\left( {{A^2} - {B^2}} \right) = \left( {A - B} \right)\left( {A + B} \right)$
$\left( {{A^3} - {B^3}} \right) = \left( {A - B} \right)\left( {{A^2} + A.B + {B^2}} \right)$
\[{A^2} - 2AB + {B^2} = {(A - B)^2}\]

Additional Information:
Cubic Equation: A cubic equation is a equation which can be represented in the form of $a{x^3} + b{x^2}cx + d$where $x$is the unknown variable and a,b,c,d are the numbers known where $a \ne 0$.If $a = 0$then the equation will become a quadratic equation and will no longer be cubic

The degree of the quadratic equation is of the order 3.

Every Cubic equation has 3 roots.

The Graph of any cubic polynomial is symmetric with respect to the inflection point of the
polynomial.

Graph to cubic polynomial ${x^3} - 9{x^2} + 27x - 27$

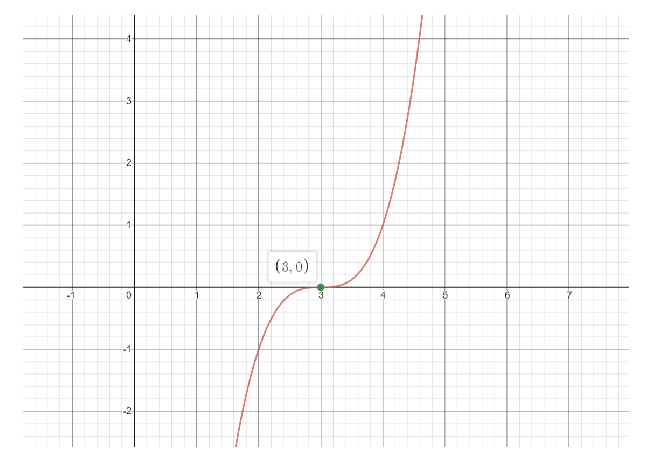
The points at which the graph touches the x-axis are the roots of the polynomial.

Note: 1. One must be careful while calculating the answer as calculation error may come.
2.Don’t forget to compare the given cubic equation with the standard one every time.