
How do you draw the graph $y={{x}^{2}}+2x$?
Answer
546.3k+ views
Hint: We find the $x-$intercepts of the curve by putting $y=0$ and we find $y-$intercept by putting $x=0$. We find the minimum value of the curve by making it a complete square. We take a minimum 5 points and join them with a free hand to get the plot.
Complete step-by-step solution:
We know that the graph of a function is the locus of points $\left( x,y \right)$ such that $y=f\left( x \right)$ where $x,y$ are real numbers. We are given the following quadratic polynomial function
\[y={{x}^{2}}+2x\]
So let us put $y=$ and find the $x-$intercept . We have
\[\begin{align}
& 0={{x}^{2}}+2x \\
& \Rightarrow x\left( x+2 \right)=0 \\
& \Rightarrow x=0\text{ or }x=-2 \\
\end{align}\]
So we find that $y=0$ at $x=0,-2$ .It means the curve cuts $x-$axis at $\left( -2,0 \right),\left( 0,0 \right)$.Let us put $x=0$ in the curve to have;
\[y={{0}^{2}}+2\cdot 0=0\]
So there is no $y-$intercept of the curve. We know that all quadratic functions of the type $y=a{{x}^{2}}+bx+c$ have minimum values but not maximum. So let us complete square in $x$ to have;
\[\begin{align}
& y={{x}^{2}}+2x \\
& \Rightarrow y={{x}^{2}}+2x+1-1 \\
& \Rightarrow y={{\left( x+1 \right)}^{2}}-1 \\
\end{align}\]
Since square is always non-negative we have ${{\left( x+1 \right)}^{2}}\ge 0$, then we have
\[\begin{align}
& \Rightarrow y={{\left( x+1 \right)}^{2}}-1\ge -1 \\
& \Rightarrow y\ge -1 \\
\end{align}\]
So the minimum value of $y=-1$ and the minimum value occurs when ${{\left( x+1 \right)}^{2}}=0$ or $x=-1$. We have already three points for the curve $\left( -2,0 \right),\left( -1,1 \right),\left( 0,0 \right)$. We find $y$ for two more points at $x=-3,x=1$ to have
\[\begin{align}
& y\left( -3 \right)={{\left( -3 \right)}^{2}}+2\left( -3 \right)=3 \\
& y\left( 1 \right)={{1}^{2}}+2\cdot 1=3 \\
\end{align}\]
So we draw the table for $x$ and $y$.
We plot the above points and join them to have the graph as
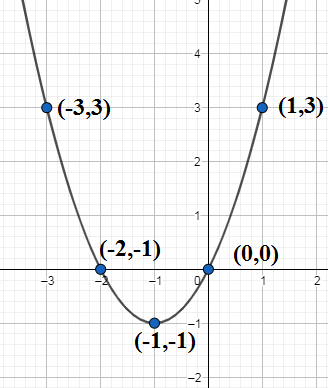
Note: We note that the obtained graph is the graph of upward parabola whose general equation is given by $y=a{{x}^{2}}+bx+c$ with the condition $a>0$ whose vertex here is $\left( -1,-1 \right)$.We can directly find the minimum value of $y={{x}^{2}}+2x$ by finding $y$ at $x=\dfrac{-b}{2a}$. If $a<0$ we the equation $y=a{{x}^{2}}+bx+c$ represents a downward parabola. We also note that the obtained curve is symmetric about the line $x=-1$.
Complete step-by-step solution:
We know that the graph of a function is the locus of points $\left( x,y \right)$ such that $y=f\left( x \right)$ where $x,y$ are real numbers. We are given the following quadratic polynomial function
\[y={{x}^{2}}+2x\]
So let us put $y=$ and find the $x-$intercept . We have
\[\begin{align}
& 0={{x}^{2}}+2x \\
& \Rightarrow x\left( x+2 \right)=0 \\
& \Rightarrow x=0\text{ or }x=-2 \\
\end{align}\]
So we find that $y=0$ at $x=0,-2$ .It means the curve cuts $x-$axis at $\left( -2,0 \right),\left( 0,0 \right)$.Let us put $x=0$ in the curve to have;
\[y={{0}^{2}}+2\cdot 0=0\]
So there is no $y-$intercept of the curve. We know that all quadratic functions of the type $y=a{{x}^{2}}+bx+c$ have minimum values but not maximum. So let us complete square in $x$ to have;
\[\begin{align}
& y={{x}^{2}}+2x \\
& \Rightarrow y={{x}^{2}}+2x+1-1 \\
& \Rightarrow y={{\left( x+1 \right)}^{2}}-1 \\
\end{align}\]
Since square is always non-negative we have ${{\left( x+1 \right)}^{2}}\ge 0$, then we have
\[\begin{align}
& \Rightarrow y={{\left( x+1 \right)}^{2}}-1\ge -1 \\
& \Rightarrow y\ge -1 \\
\end{align}\]
So the minimum value of $y=-1$ and the minimum value occurs when ${{\left( x+1 \right)}^{2}}=0$ or $x=-1$. We have already three points for the curve $\left( -2,0 \right),\left( -1,1 \right),\left( 0,0 \right)$. We find $y$ for two more points at $x=-3,x=1$ to have
\[\begin{align}
& y\left( -3 \right)={{\left( -3 \right)}^{2}}+2\left( -3 \right)=3 \\
& y\left( 1 \right)={{1}^{2}}+2\cdot 1=3 \\
\end{align}\]
So we draw the table for $x$ and $y$.
| $x$ | $y$ |
| $-3$ | 3 |
| $-2$ | 0 |
| $-1$ | $-1$ |
| 0 | 0 |
| 1 | 1 |
We plot the above points and join them to have the graph as

Note: We note that the obtained graph is the graph of upward parabola whose general equation is given by $y=a{{x}^{2}}+bx+c$ with the condition $a>0$ whose vertex here is $\left( -1,-1 \right)$.We can directly find the minimum value of $y={{x}^{2}}+2x$ by finding $y$ at $x=\dfrac{-b}{2a}$. If $a<0$ we the equation $y=a{{x}^{2}}+bx+c$ represents a downward parabola. We also note that the obtained curve is symmetric about the line $x=-1$.
Recently Updated Pages
Master Class 11 Social Science: Engaging Questions & Answers for Success

Master Class 11 Physics: Engaging Questions & Answers for Success

Master Class 11 Maths: Engaging Questions & Answers for Success

Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 Computer Science: Engaging Questions & Answers for Success

Master Class 11 Chemistry: Engaging Questions & Answers for Success

Trending doubts
What is meant by exothermic and endothermic reactions class 11 chemistry CBSE

10 examples of friction in our daily life

Difference Between Prokaryotic Cells and Eukaryotic Cells

1 Quintal is equal to a 110 kg b 10 kg c 100kg d 1000 class 11 physics CBSE

One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

Draw a diagram of nephron and explain its structur class 11 biology CBSE




