Question

How do you draw the graph of $ 2x+3y=12 $ ?

Answer 1

Hint: In the given question, we have given an equation of a line as $ 2x+3y=12 $ , which is a straight-line equation. In order to draw a graph of the given equation, we will need to write the equation in a slope intercept form. A straight-line equation is always linear and represented as $ y=mx+c $ where $ m $ is the slope of the line and $ c $ is the y-intercept and $ \dfrac{-c}{m} $ is the x-intercept.
Now, getting the points we can easily plot the graph of the given straight line equation.

Complete step-by-step answer:
We have equation of line,
 $ 2x+3y=12 $
Subtracting 2x from both the sides of the equation,
 $ 3y=-2x+12 $
Dividing both the sides by 3, we will get
 $ y=-\dfrac{2}{3}x+4 $
Rewrite the above equation in a slope intercept form, i.e. $ y=mx+c $
 $ y=-\dfrac{2}{3}x+4 $
Now we compare this given equation with the general linear equation i.e., $ y=mx+c $
Hence ,
Slope of the given line, $ m=-\dfrac{2}{3} $ .
y-intercept of the given line , $ c=4 $ .
Therefore, we can say that point $ (0,4) $ lie on the line.
x-intercept of the given line , $ \dfrac{-c}{m}=-\dfrac{4}{\dfrac{-2}{3}}=-\dfrac{4}{1}\times -\dfrac{3}{2}=6 $ .
Therefore, we can say that point $ (6,0) $ lie on the line.
With the help of two points, we can plot the graph by connecting the points as follow,

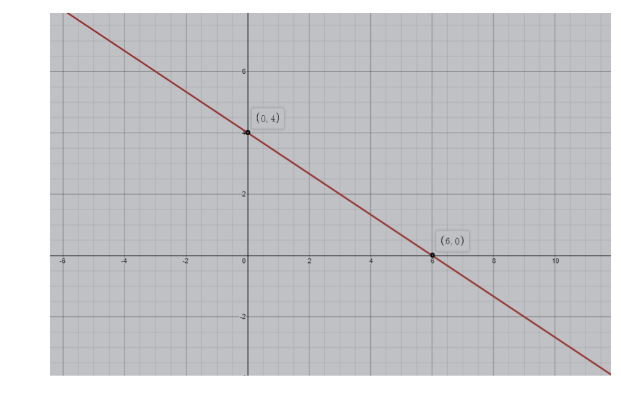
Note: Slope of a line can also be found if two points on the line are given. Let the two points on the line be $ ({{x}_{1}},{{y}_{1}}),({{x}_{2}},{{y}_{2}}) $ respectively.
Then slope is given by, $ m=\dfrac{{{y}_{2}}-{{y}_{1}}}{{{x}_{2}}-{{x}_{1}}} $ .
Slope is also defined as the ratio of change in $ y $ over the change in $ x $ between any two points.
 y-intercept can also be found by substituting $ x=0 $ .
Similarly, x-intercept can also be found by substituting $ y=0 $ .