Answer
Verified434.4k+ views
Hint: This problem deals with the derivation of the law of cosines. The law of cosines is for calculating one side of a triangle when the angle is opposite and the other two sides which are known. Here let the unknown side be \[c\], and the angle opposite angle to this side is $\alpha $, and the other two sides are $a$ and $b$, from here we can derive the law of cosines.
Complete Step by Step Solution:
In trigonometry, the law of cosines relates the lengths of the sides of a triangle to the cosine of one of its angles. Using the notations as given in the above hint, the law of cosines states where $\alpha $ denotes the angle contained between sides of lengths $a$ and $b$ and the opposite side of length $c$.
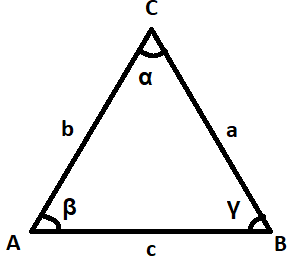
Then the law of cosines is given by:
\[ \Rightarrow {c^2} = {a^2} + {b^2} - 2ab\cos \alpha \]
Here $a,b$ and $c$ are the sides of the triangle and $\alpha $is the angle between the sides $b$and $c$.
This can be applied to any triangle.
If the unknown side is $a$ and the angle opposite to this side is the angle is $\beta $, where the other two sides are known $b$ and $c$. Then using the law of cosines, the side $a$ is given by:
\[ \Rightarrow {a^2} = {b^2} + {c^2} - 2bc\cos \beta \]
If the unknown side is $b$ and the angle opposite to this side is the angle is $\gamma $, where the other two sides are known $a$ and $c$. Then using the law of cosines, the side $b$ is given by:
\[ \Rightarrow {b^2} = {a^2} + {c^2} - 2ac\cos \gamma \]
Note: Please note that the law of cosines is used here to find the unknown side of a triangle, this can be used to find the unknown angle which is given by:
$ \Rightarrow \cos \alpha = \dfrac{{{a^2} + {b^2} - {c^2}}}{{2ab}}$
Law of sines is used to find all the sides of the triangle and all the angles of the triangle, given by:
$ \Rightarrow \dfrac{a}{{\sin \beta }} = \dfrac{b}{{\sin \gamma }} = \dfrac{c}{{\sin \alpha }}$
Complete Step by Step Solution:
In trigonometry, the law of cosines relates the lengths of the sides of a triangle to the cosine of one of its angles. Using the notations as given in the above hint, the law of cosines states where $\alpha $ denotes the angle contained between sides of lengths $a$ and $b$ and the opposite side of length $c$.
Then the law of cosines is given by:
\[ \Rightarrow {c^2} = {a^2} + {b^2} - 2ab\cos \alpha \]
Here $a,b$ and $c$ are the sides of the triangle and $\alpha $is the angle between the sides $b$and $c$.
This can be applied to any triangle.
If the unknown side is $a$ and the angle opposite to this side is the angle is $\beta $, where the other two sides are known $b$ and $c$. Then using the law of cosines, the side $a$ is given by:
\[ \Rightarrow {a^2} = {b^2} + {c^2} - 2bc\cos \beta \]
If the unknown side is $b$ and the angle opposite to this side is the angle is $\gamma $, where the other two sides are known $a$ and $c$. Then using the law of cosines, the side $b$ is given by:
\[ \Rightarrow {b^2} = {a^2} + {c^2} - 2ac\cos \gamma \]
Note: Please note that the law of cosines is used here to find the unknown side of a triangle, this can be used to find the unknown angle which is given by:
$ \Rightarrow \cos \alpha = \dfrac{{{a^2} + {b^2} - {c^2}}}{{2ab}}$
Law of sines is used to find all the sides of the triangle and all the angles of the triangle, given by:
$ \Rightarrow \dfrac{a}{{\sin \beta }} = \dfrac{b}{{\sin \gamma }} = \dfrac{c}{{\sin \alpha }}$