Question

How do you derive the law of cosine?

Answer 1

Hint: the law of cosines implies the relation between the lengths of sides of a triangle with respect to the cosine of its angle.in a right angle triangle cosine of an angle is the length of the adjacent side divided by the length of the hypotenuse.to derive the law of cosine we will use trigonometric functions and their property. The trigonometry functions are the real functions which relate an angle of a right angled triangle to the ratio of two side lengths. We will use the Pythagorean Theorem to prove the law of cosine. The cosine is a periodic function having period of $2\pi $.The Pythagoras theorem is categorized by the formula for the law of cosines. The Pythagoras theorem is a fundamental relation in Euclidean geometry in the three sides of the triangle. In a triangle if $a,b,$and $c$ are the sides of the triangle and $A$is the angle between sides $b$ and $c$ then,
According to cosine law,
${a^2} = {b^2} + {c^2} - 2bc\cos A$
If $B$ and $C$ is the angle between sides $\left( {ca} \right)$ and $\left( {ab} \right)$ respectively then,
${b^2} = {a^2} + {c^2} - 2ac\cos B$
${c^2} = {b^2} + {a^2} - 2bc\cos C$

Complete step by step answer:
Step: 1

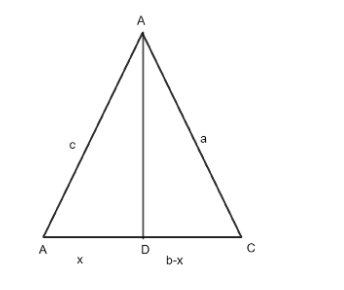
Consider the triangle ADB ,
Take cosine in the triangle ADB,
$
   \Rightarrow \cos A = \dfrac{x}{c} \\
   \Rightarrow x = c\cos A \\
 $
Step: 2 use Pythagoras theorem in the triangle ADB,
$
   \Rightarrow {x^2} + {h^2} = {c^2} \\
   \Rightarrow {h^2} = {c^2} - {x^2} \\
 $
Use the Pythagoras theorem in the triangle CDB,
$ \Rightarrow {\left( {b - x} \right)^2} + {h^2} = {a^2}$
Substitute the value of ${h^2} = {c^2} - {x^2}$ in the equation ${\left( {b - x} \right)^2} + {h^2} = {a^2}$.
$
   \Rightarrow {a^2} = {\left( {b - x} \right)^2} + \left( {{c^2} - {x^2}} \right) \\
   \Rightarrow {a^2} = {b^2} - 2bx + {x^2} + {c^2} - {x^2} \\
   \Rightarrow {a^2} = {b^2} - 2bx + {c^2} \\
 $
Substitute the value of $x = c\cos A$ in the equation.
$
   \Rightarrow {a^2} = {b^2} - 2b\left( {c\cos A} \right) + {c^2} \\
   \Rightarrow {a^2} = {b^2} + {c^2} - 2bc\cos A \\
 $

Note: Using the law of cosine we can find the unknown angle. If the angle between sides are equal to 90 then cosine rule will satisfy the Pythagoras theorem. Students are advised to draw the triangle and derive the law of cosine. They must use the cosine formula to prove the rule. They should know to apply Pythagoras theorem in the triangle. Students are advised to derive the rule of cosine step by step.