Question

How do you convert $y = - 3$ to polar form?

Answer 1

Hint:First find the conversion formula between Cartesian coordinate system and the polar coordinate system and then replace $y$ with its polar form. Polar form consists of “r” and “$\theta $” as its coordinates where “r” is the distance from the origin and “$\theta $” represents the angle of the particular coordinate in the anti clockwise direction with the positive x-axis. Use this information to derive the relation between polar and Cartesian coordinate systems.

Complete step by step answer:
system in order to convert $y = - 3$ to polar form.Let us consider a point P having Cartesian coordinates $(x,\,y)$ and having polar coordinates $(r,\;\theta )$. It can be represented through a figure as follows:

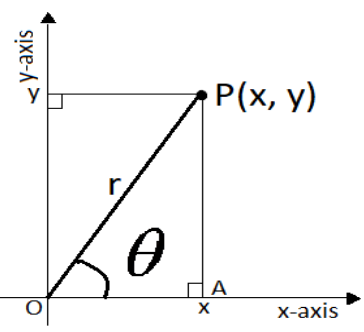
We can see in the figure that “r” is the distance of the point P from the origin and “$\theta $” is the angle of the point in an anticlockwise direction with x-axis. From the figure, in the right angled $\Delta {\text{OPA}}$. From trigonometric relations we can write,
$
\dfrac{y}{r} = \sin \theta \;{\text{and}}\;\dfrac{x}{r} = \cos \theta \; \\
\Rightarrow y = r\sin \theta \;{\text{and}}\;x = r\cos \theta \\ $
Also, from Pythagoras theorem,
$r = \sqrt {{x^2} + {y^2}} $
So we have the following relations between polar and Cartesian coordinate system
$
r = \sqrt {{x^2} + {y^2}} \\
\Rightarrow y = r\sin \theta \;{\text{and}}\;x = r\cos \theta \\ $
We want the value of $y$ for this problem, that is $y = r\sin \theta $

Therefore $y = - 3$ will be written in polar form as $r\sin \theta = - 3$.

Note:The above conversional results are useful in converting polar coordinates into Cartesian coordinates; also you can derive yourself the conversion formula for Cartesian coordinates to polar form with use of some trigonometry. Major difference between the Cartesian and polar coordinate system is that the Cartesian coordinate system is valid in three dimension coordinates too but polar is not.