Question

How do you classify $4{{x}^{2}}+9{{y}^{2}}=36$?

Answer 1

Hint: To solve this question we need to know the general equation of an ellipse which is $\dfrac{{{\left( x-h \right)}^{2}}}{{{a}^{2}}}+\dfrac{{{\left( y-k \right)}^{2}}}{{{b}^{2}}}=1$. To convert the given equation into its general form, it is important to divide the equation by 36 and solve further to get the desired result. Then, we will use $4={{2}^{2}},9={{3}^{2}}$ in the solution.

Complete step by step solution:
Any kind of an oval shaped like structure is what we call an ellipse. To know how the given equation forms an ellipse, we are going to simplify it.
For this we will consider $4{{x}^{2}}+9{{y}^{2}}=36$. At this step we will divide the whole equation by 36. Therefore, we get
$\begin{align}
  & 4{{x}^{2}}+9{{y}^{2}}=36 \\
 & \Rightarrow \dfrac{4{{x}^{2}}}{36}+\dfrac{9{{y}^{2}}}{36}=1 \\
 & \Rightarrow \dfrac{{{x}^{2}}}{9}+\dfrac{{{y}^{2}}}{4}=1 \\
 & \Rightarrow \dfrac{{{x}^{2}}}{{{3}^{2}}}+\dfrac{{{y}^{2}}}{{{2}^{2}}}=1\,\,\left[ \because 4={{2}^{2}},9={{3}^{2}} \right] \\
\end{align}$
We can also write the equation $\dfrac{{{x}^{2}}}{{{3}^{2}}}+\dfrac{{{y}^{2}}}{{{2}^{2}}}=1$ as $\dfrac{{{\left( x-0 \right)}^{2}}}{{{3}^{2}}}+\dfrac{{{\left( y-0 \right)}^{2}}}{{{2}^{2}}}=1$ which is the actual general form of an ellipse, $\dfrac{{{\left( x-h \right)}^{2}}}{{{a}^{2}}}+\dfrac{{{\left( y-k \right)}^{2}}}{{{b}^{2}}}=1$. This is why the given equation is classified as an ellipse. Now, we will draw its figure for surety. This ellipse will take an area of 3 units of x-axis and 2 units of y-axis. Therefore, we get the following figure of it.
 

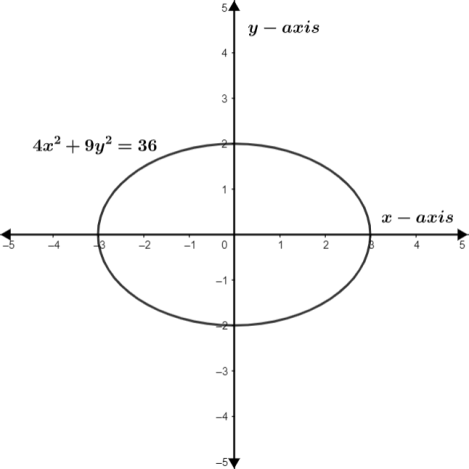
Hence, the equation $4{{x}^{2}}+9{{y}^{2}}=36$ has a classification of an ellipse only.

Note: We could have used the help of substitution in which we can substitute the values of x and get the values of y. For example, take x = 0 which gives,
\[\begin{align}
  & 4{{\left( 0 \right)}^{2}}+9{{y}^{2}}=36 \\
 & \Rightarrow 9{{y}^{2}}=36 \\
 & \Rightarrow {{y}^{2}}=4 \\
 & \Rightarrow y= \pm 2 \\
\end{align}\]
This gives the points as (0, 2) and (0, -2). Similarly, we can collect points and plot them on the graph. After doing so we will be able to figure out the correct figure of the given equation and classify it accordingly. The best way to simplify such an equation is to divide it with a constant term in it. For example, we have divided the equation $4{{x}^{2}}+9{{y}^{2}}=36$ by 36. Out of a and b, the one with the greater length or unit will be considered as the major axis.