Question

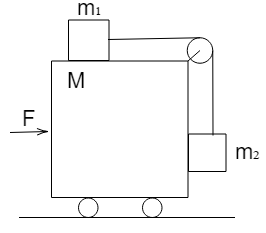
What horizontal force $F$ must be applied to the cart shown in the figure, so that block remains stationary with respect to cart. Assume all surfaces as frictionless.
$(A)\dfrac{{(M + {m_1} + {m_2}){m_2}g}}{{{m_1}}}$
$(B)\dfrac{{(M + {m_1} + {m_2}){m_1}g}}{{{m_2}}}$
$(C)m \times \dfrac{{{m_2}g}}{{{m_1}}}$
$(D)M \times \dfrac{{{m_1}g}}{{{m_2}}}$

Answer 1

Hint: In order to solve this question, first we will make the free body diagram of all the masses. Then we will apply the concept of $\sum F = ma$. Then we will find out the acceleration with the help of the force equations acting on the two blocks and then with the help of acceleration and mass, we will find the required force.


Complete step by step solution:
In this particular question we will be using the concept that $\sum F = ma$ and thus, we also draw the free body diagram for ${m_1}$, ${m_2}$ and the whole system of masses. It is important to note that the normal force always acts in a direction perpendicular to the direction of the contacting force, we will draw ${n_1}$​ and ${n_2}$​ as shown in the figure. Also, note that the block ${m_2}$​ is kept in contact with the cart, and this means that it feels a normal force which is exerted by the cart. The ropes always pull the bodies towards the centre of the rope, so we will draw the tension force $T$. Lastly, we will draw the gravitational force which is acting on each block, which always points in the downward direction. So, the free body diagram for this question will be:

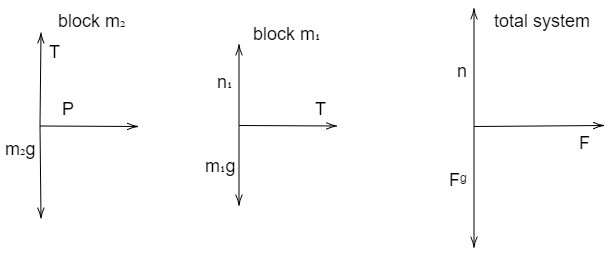
We know that $\sum F = ma$
On applying this concept on the block ${m_1}$, we get,
$T = {m_1}a......(1)$
Similarly, on applying the same concept on the block ${m_2}$, we get,
$T - {m_2}g = 0$
$T = {m_2}g.....(2)$
On comparing equation (1) and (2), we get,
${m_1}a = {m_2}g$
$a = \dfrac{{{m_2}g}}{{{m_1}}}$
The horizontal force $F$ must be applied to the cart so that block remains stationary with respect to cart is,
$F = {m_{total}} \times a$
On putting ${m_{total}} = {m_1} + {m_2} + M$ and $a = \dfrac{{{m_2}g}}{{{m_1}}}$, we get,
$F = \dfrac{{(M + {m_1} + {m_2}){m_2}g}}{{{m_1}}}$
So, the final answer is $(A)\dfrac{{(M + {m_1} + {m_2}){m_2}g}}{{{m_1}}}$.

Note:
It is important to note that in the question, it has been mentioned to assume all the surfaces to be frictionless. Completely frictionless surfaces are not available and they are hypothetical but in order to make the problems simple such assumptions are made.