Question

How many horizontal asymptotes can the graph of $y=f(x)$ have?

Answer 1

Hint: In this question, we have to find the number of horizontal asymptotes of an equation. As we know, a horizontal asymptote is a horizontal line that expresses a function, where x tends towards $\infty $ or $-\infty $ . Also, the horizontal asymptote is parallel to the x-axis. So, to solve this problem we will take three different cases. The first case is to take a function such that the growth rate of the numerator increases faster than the denominator. The second case is when the growth rate of the denominator increases faster than the numerator. While the third case when both the numerator and the denominator differ by a constant. Thus, in all three cases we draw the graph, which helps to understand the number of the horizontal asymptotes in each function.

Complete step by step answer:
According to the question, we have to find the number of horizontal asymptotes. As we know, a horizontal asymptote is a horizontal line that expresses a function, where x tends towards $\infty $ or $-\infty $ .
Thus, to solve this problem, we will take three different cases to get to know about the horizontal asymptotes.
Case 1:
We will take a function, such that the growth rate of the numerator increases faster than the denominator, that is
Let $y={{x}^{2}}$ -------- (1)
Thus, we see that the denominator of equation (1) is 1, and the numerator is ${{x}^{2}}$ , which means if x is any real number it is always greater than 1.
Thus, the graph for equation (1) is:

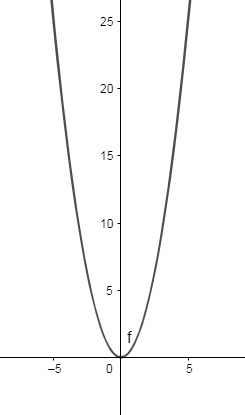
Thus, we see that there is no horizontal line that is parallel to the x-axis. Implies for the equation where the growth rate of the numerator is faster than the denominator, there are no horizontal asymptotes.
Case 2:
We will take a function, such that the growth rate of the denominator increases faster than the numerator, that is
Let $y=\dfrac{1}{x}$ -------- (2)
Thus, we see that the denominator of equation (2) is x, and the numerator is 1 , which means if x is any real number it is always greater than 1.
Thus, the graph for equation (2) is:

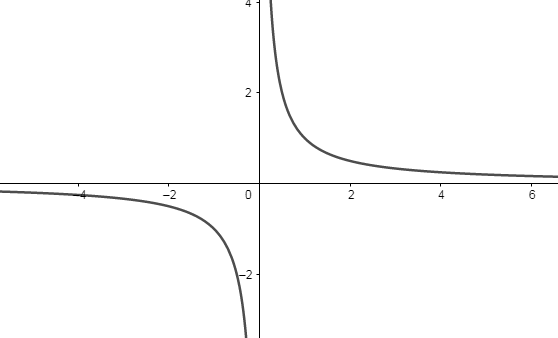
Thus, we see that there is one horizontal line that is parallel to the x-axis. Implies for the equation where the growth rate of the numerator is slower than the denominator, there are only horizontal asymptotes.
Case 3:
We will take a function, such that the growth rate of the denominator and numerator differ by a constant, that is
Let $y=c$ -------- (3)
Thus, we see that the function of equation (3) is constant.
Thus, the graph for equation (3) is:

Thus, we see that there we can draw two horizontal lines that are parallel to the x-axis. Implies, there are only two horizontal asymptotes.
Therefore, we see that for the function $y=f(x)$, we have three different cases and all cases have the different numbers of horizontal asymptotes.

Note:
While solving this problem, keep in mind that we have to find the number of horizontal asymptotes, which is a horizontal line parallel to a x-axis. Also, do not forget to do all three cases. Each case is important because we have to find the number of horizontal asymptotes of a $y=f(x)$