Question

What is the height of the cone which is formed by joining the two ends of a sector of circle with radius r and angle $60{}^\circ $ .
(A). $\dfrac{\sqrt{35}}{6}r$
(B). $\dfrac{\sqrt{25}}{6}r$
(C). $\dfrac{r}{\sqrt{3}}$
(D). $\dfrac{{{r}^{2}}}{\sqrt{3}}$

Answer 1

Hint: Focus on the point that area of the circle of radius r is equal to the curved/lateral surface area of the cone formed using the sector and radius of the circle is the slant height of the cone.

Complete step-by-step solution -
Let us start by drawing a representative figure of the sector and the cone..

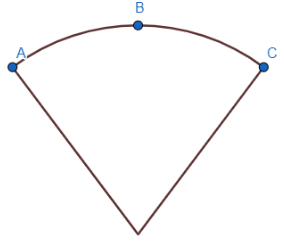
Now, if we join the points A and C of the sector, we get a cone with slant height equal to r and curved surface area equal to the area of the sector.

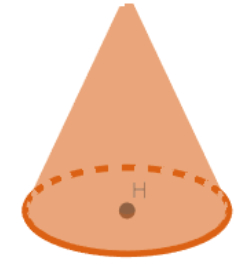
Let the height of the cone be h units and radius be x units.
Now, we know that the slant height of the cone is equal to the root of the squares of the height and the radius.
$\therefore l=\sqrt{{{x}^{2}}+{{h}^{2}}}$
Also, from the question, we have deduced that slant height is equal to r.
  $\therefore r=\sqrt{{{x}^{2}}+{{h}^{2}}}..................(i)$
Now, as we know that the curved surface area of the cone is equal to the area of the sector, the equation we get is:
Curved surface area of cone = area of the sector.
$\pi xl=\dfrac{\theta }{360}\pi {{r}^{2}}$
$\Rightarrow xl=\dfrac{60}{360}{{r}^{2}}$
As we mentioned earlier, the slant height of the cone is equal to r. So, using the value in our equation, we get
 $xr=\dfrac{60}{360}{{r}^{2}}$
$\Rightarrow x=\dfrac{1}{6}r$
Now if we substitute the value of x in equation (i), we get
$r=\sqrt{{{\left( \dfrac{1}{6}r \right)}^{2}}+{{h}^{2}}}$
Now we will square both sides of the equation. On doing so, we get
${{r}^{2}}={{\left( \dfrac{1}{6}r \right)}^{2}}+{{h}^{2}}$
$\Rightarrow {{h}^{2}}=\dfrac{35}{36}{{r}^{2}}$
$\Rightarrow h=\sqrt{\dfrac{35}{36}{{r}^{2}}}$
$\Rightarrow h=\dfrac{\sqrt{35}}{6}r$ units
Hence, the answer to the above question is option (a).

Note: Make sure to convert all the dimensions to a standardized system of units; this decreases the chance of errors. Also, you need to remember all the basic formulas for surface area and volume of the general 3-D shapes like the cone, cube, cylinder, etc.