Question

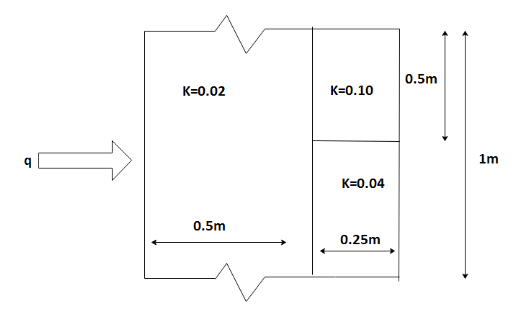
Heat flows through a composite slab, as shown. The depth of the slab is 1 m. The k values are in W/mK, then the overall thermal resistance in K/W is

A. 17
B. 21.9
C. 28.6
D. 39.2

Answer 1

Hint:We shall take the thermal resistances in the figure and the two thermal resistances of value 0.1 W/mK and 0.04 W/mK are parallel to each other and the equivalent resistance of these is in series with the 0.02 W/mK thermal resistors. Though, we will first find the resistance using the value of the conductivities.

Complete step by step answer:
As there is no variation in the horizontal direction, we shall consider the portion of the slab that is 1 m deep and 1 m high and since it represents the entire wall. Here, we shall also assume that for any cross-section of the slab which is normal to the x - direction to be isothermal, the thermal resistance network for the slab is shown in the figure. When we take the thermal resistance of the network in correspondence to the figure given, we can see that there are two resistors ${R_2}$ and ${R_3}$ parallel to each other between points B and C and they are connected in series with resistor ${R_1}$.

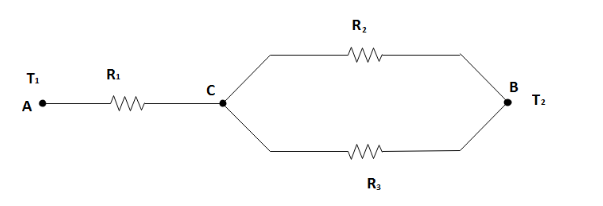
We know that the lengths ${L_1}$, ${L_2}$ and ${L_3}$ are given in the figure. Thus, the individual resistances obtained from the above figure are as follows for the conductivity constants ${K_1}$,${K_2}$,${K_3}$ as follows:
\[
{R_1} = \dfrac{{{L_1}}}{{{A_1}{K_1}}} \\
\Rightarrow {R_1} = \dfrac{{0.5}}{{0.02(1)}} \\
\therefore {R_1} = 25\Omega \\ \]
Similarly, we get the other two resistances as follows:
\[
{R_2} = \dfrac{{{L_2}}}{{{A_2}{K_2}}} \\
\Rightarrow {R_2} = \dfrac{{0.25}}{{0.1(0.5 \times 1)}} \\
\therefore {R_2} = 5\Omega \\ \]
\[
\Rightarrow{R_3} = \dfrac{{{L_3}}}{{{A_3}{K_3}}} \\
\Rightarrow {R_3} = \dfrac{{0.25}}{{0.04(0.5 \times 1)}} \\
\therefore {R_2} = 5\Omega \\ \]
Now, ${R_2}$ and ${R_3}$ are in parallel while ${R_1}$ and so their equivalent resistance will be as follows:
\[
R={{R}_{1}}+\dfrac{{{R}_{2}}{{R}_{3}}}{{{R}_{2}}+{{R}_{3}}} \\
\Rightarrow R=25+\dfrac{5\centerdot (12.5)}{5+12.5} \\
\therefore R=28.6\dfrac{K}{W} \\
\]
Hence C is the correct answer.

Note:When the resistances are connected in parallel, the voltage remains constant and the net resistance is lower than the smallest resistance of the network, while when they are connected in series, the current remains constant and the net resistance is higher than the largest resistance of the network.