Question

What happens to the reading $ A_1,A_2,A_3 $ and $ A $ when the bulb $ B_2 $ gets fused?

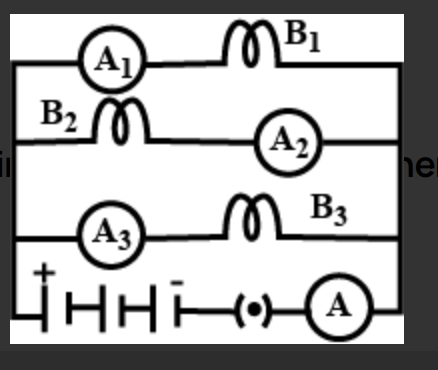
 $ \left( A \right)A_1 = 1A,A_2 = 0A,A_3 = 0AandA = 2A \\
\left( B \right)A_1 = 1A,A_2 = 0A,A_3 = 1AandA = 2A \\
\left( C \right)A_1 = 2A,A_2 = 0A,A_3 = 1AandA = 2A \\
\left( D \right)A_1 = 1A,A_2 = 0A,A_3 = 1AandA = 1A \\ $

Answer 1

Hint :In order to solve this question, we are going to take the voltage and the current, and then find the total resistance for the circuit, then considering the case when the bulb $ B_2 $ gets fused, we can find the corresponding resistance and the voltage. And finally the ampere readings are found.
In the parallel setup of resistances, the total resistance for all the resistors is given by $ \dfrac{1}{R} = \dfrac{1}{{R_1}} + \dfrac{1}{{R_2}} + \dfrac{1}{{R_3}} $
Here, all the bulbs are same so they have the same values of resistances, so, $ R_1 = R_2 = R_3 = R $

Complete Step By Step Answer:
The total resistance will be $ R' = \dfrac{R}{3} $
Now as we know that according to ohm’s law
 $ V = IR $
Where $ V $ is the voltage, $ I $ is the current and $ R $ is the resistance of the circuit
In this case, the voltage is given as $ 4.5V $ and the current across the resistances is $ 3A $
Substituting this information in the formula, we get
 $ 4.5 = 3 \times \dfrac{R}{3} \\
   \Rightarrow R = 4.5\Omega \\ $
But as the bulb $ B_2 $ gets fused, only two bulbs will remain connected in parallel
Therefore, the resultant resistance will be

 $ \dfrac{1}{{R'}} = \dfrac{1}{{R_1}} + \dfrac{1}{{R_2}} = \dfrac{2}{{4.5}} \\
   \Rightarrow R' = \dfrac{{4.5}}{2}\Omega \\ $
So, the current will be equal to
 $ I = \dfrac{V}{{R'}} = \dfrac{{2 \times 4.5}}{{4.5}} = 2A $
Since $ B_2 $ gets fused and only $ B_1 $ and $ B_3 $ are parallel and have the same resistance, $ 2A $ current will be equally distributed between them with the currents equal to $ 1A $ to each.
Hence, the ammeter readings will be like where $ A_1 $ shows $ 1A $ , $ A_2 $ shows zero where the bulb $ B_2 $ blows off, $ A_3 $ shows $ 1 $ ampere and $ A $ shows $ 2 $ amperes, the total current in the circuit.
So, option (B) is correct.

Note :
It is important to note that it is given a parallel combination of the resistors and the current from each parallel section will be different while the voltage will be the same for the resistances as given. When bulb $ B_2 $ blows off, the segment will be short circuited and no current will pass through that segment.