Question

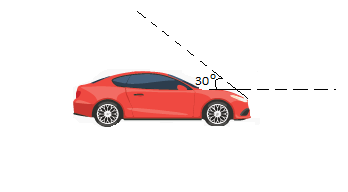
Hailstones falling vertically with speed of $10m/\sec $. They hit the windscreen of the moving car and rebound elastically. Windscreen makes ${30^ \circ }$ angle with the horizontal. What will be the velocity of car if the driver finds the hailstones rebound vertically after striking?

Answer 1

Hint: The hailstones move vertically upward from the observation of driver. The velocity of hailstones is equal to the summation of velocity of hailstones with respect to car and velocity of car.
When hailstones fall vertically down then, the velocity of hailstones will be equal to zero.

Complete Step by Step Solution: -
Under the observation of the driver, according to the question, it is given that hailstones after the elastic collision move vertically upward.
Now, let the velocity of hailstones be ${v_h}$ , velocity of hailstones with respect to car be ${v_{h,c}}$ and velocity of car be ${v_c}$.
Then, the velocity of hailstones can be given by the addition of velocity of hailstones with respect to car and velocity of car –
${\vec v_h} = {\vec v_{h,c}} + {\vec v_c}$
Therefore, when they fall vertically down –
So, velocity of hailstones will be equal to zero
${\left( {{{\vec v}_h}} \right)_x} = {\left( {{{\vec v}_{h,c}} + {{\vec v}_c}} \right)_x}$
But, ${\vec v_h} = 0$
We know that,
${\left( {{{\vec v}_h}} \right)_x} = - \left( {v\cos {{30}^ \circ }} \right)$
Because windscreen makes an angle of ${30^ \circ }$ with the horizontal
$\therefore {\left| {{{\vec v}_c}} \right|_x} = {\left| {{{\vec v}_{h,c}}} \right|_x}$
Now, at $y - axis$, we get –
${\left( {{{\vec v}_h}} \right)_y} = {\left( {{{\vec v}_{h,c}} + {{\vec v}_c}} \right)_y} \cdots \left( 1 \right)$
Since, it is given that, velocity if hailstones are falling vertically with speed of $10m/\sec $
$\therefore {\left( {{v_h}} \right)_y} = - 10m/\sec $
Then, ${\left( {{v_c}} \right)_y} = 0$
Putting above two values in equation $\left( 1 \right)$, we get –
$
   - 10 = - V\sin {30^ \circ } + 0 \\
  V\sin {30^ \circ } = 10 \\
  V \times \dfrac{1}{2} = 10 \\
  V = 20m/\sec \\
 $
As we have already seen above –
$
  {\left( {{{\vec v}_c}} \right)_x} = V\cos {30^ \circ } \\
  {\left( {{{\vec v}_c}} \right)_x} = 20 \times \dfrac{{\sqrt 3 }}{2} \\
  {\left( {{{\vec v}_c}} \right)_x} = 10\sqrt 3 m/\sec \\
  {{\vec v}_c} = 10\sqrt 3 m/\sec \\
 $
Therefore, the velocity of car if the driver finds the hailstones rebound vertically after striking is $10\sqrt 3 m/\sec $.

Note: Elastic collision can be defined as the collision which occurs between two bodies and the total kinetic energy in the system remains constant. In an ideal, perfectly elastic collision, there is no net conversion of kinetic energy into other forms such as heat, noise, or potential energy.