Question

Green light is incident at the polarising angle on a certain transparent medium. The angle of refraction is $30^\circ $.Find
i) Polarising angle, and
ii) Refractive index of medium.

Answer 1

Hint: Just remember, When light is incident at the polarising angle of a medium, the part of the light is reflected and becomes polarised. Some part of the ray is refracted and becomes slightly polarised. The $\tan $ of the polarising angle is simply the refractive index of the medium.

Complete step by step solution:
This situation can be best described by the following diagram.

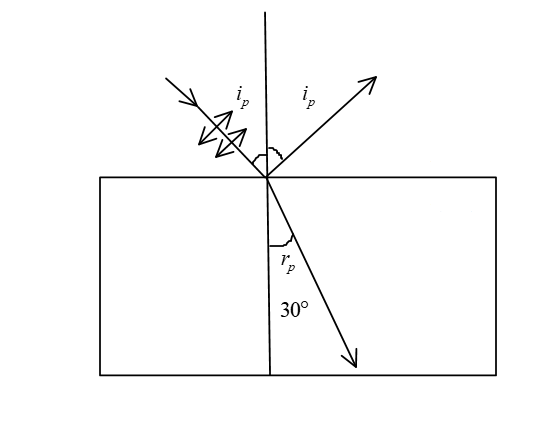
Here, the incident light is at a polarizing angle on the transparent medium. First, we need to realize what happens when light is incident at a polarizing angle and what is a polarizing angle.
The Polarizing angle is the angle of incidence such that, after the incidence, the refracted ray and the reflected ray makes an angle of ${90^ \circ }$. When an unpolarised light is incident on the glass, the reflected light will be perfectly polarised and refracted light will be slightly polarised.
i) Now, as we can see in the diagram, the reflected and refracted ray make an angle of ${90^ \circ }$, by simple geometry, we can write:
${i_p} + {r_p} = {90^ \circ }$, or
$ \Rightarrow {i_p} = {90^ \circ } - {r_p}$
Here, the angle of refraction is given, ${r_p} = 30^\circ $. Hence we can simply find the angle of incidence or polarizing angle ${i_p}$ by,
${i_p} = {90^ \circ } - {30^\circ } = 60^\circ $

Therefore, the polarizing angle or the angle of incidence is $60^\circ$.

ii) Refractive index
Now we know that,
${i_p} + {r_p} = {90^ \circ }$
Where, ${i_p}$ is the angle of incidence and ${r_p}$ is the angle of refraction. Hence we can apply Snell’s law which states that,
${n_1}\sin {i_p} = {n_2}\sin {r_p}$
Where, ${n_1}$ and ${n_2}$ are the refractive indices of the medium 1 and 2.
Now, we also know that, ${r_p} = {90^ \circ } - {i_p}$ , on substituting ${r_p}$ in the Snell’s law equation, we get,
${n_1}\sin {i_p} = {n_2}\sin ({90^ \circ } - {i_p})$, or
$ \Rightarrow {n_1}\sin {i_p} = {n_2}\cos {i_p}$
Hence, finally, we can write the refractive index of the medium as given below,
$\mu = \dfrac{{{n_2}}}{{{n_1}}} = \tan {i_p}$
Now, we have derived the formula for the refractive index, we can simply put the value of ${i_p}$ and get the result.
$\mu = \tan {60^ \circ } = 1.732$

Therefore, the refractive index of the medium is 1.732

Note: The polarizing angle is also known as Brewster’s angle. It is important to note that the angle between the refracted and reflected ray is ${90^ \circ }$. The reflected ray is completely polarised as opposed to the refracted ray which is slightly polarised.