Question

How do you graph $y=\sin \left( \dfrac{1}{3}x \right)$ ?

Answer 1

Hint: In order to graph any function, we must know an ample number of points on it in order to trace it through them. Some of which are the stationary and critical points and the points of inflection. Inflection points are those where the second derivative of the graph is zero. We must also know the intervals between the critical and inflection point and whether the function is increasing or decreasing in these intervals.

Complete step-by-step answer:
For the function $f\left( x \right)=\sin \left( \dfrac{1}{3}x \right)$, the amplitude of this function remains the same, that is, 1 but the period changes.
For any sinusoidal function, $f\left( x \right)=A\sin Bx$, $A$ represents the amplitude of sine function and $\dfrac{2\pi }{B}$ represents the period of the sine function.
Since $B=\dfrac{1}{3}$, therefore, for $f\left( x \right)=\sin \left( \dfrac{1}{3}x \right)$, the period is equal to $\dfrac{2\pi }{\dfrac{1}{3}}=6\pi $. Thus, the graph starts repeating itself after $6\pi $.

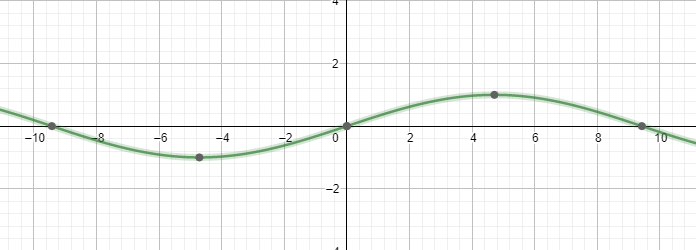
Let us take five points in one period on this graph now.
$\begin{align}
  & {{x}_{1}}=0 \\
 & {{x}_{2}}=\dfrac{3\pi }{2} \\
 & {{x}_{3}}=3\pi \\
 & {{x}_{4}}=\dfrac{9\pi }{2} \\
\end{align}$
${{x}_{5}}=6\pi $
Now, put the x-coordinate of these points in the function $y=\sin \left( \dfrac{1}{3}x \right)$ to find the y-coordinate of the points.
When ${{x}_{1}}=0,$ ${{y}_{1}}=\sin \left( \dfrac{1}{3}.0 \right)=\sin 0=0$
When ${{x}_{2}}=\dfrac{3\pi }{2},$ ${{y}_{2}}=\sin \left( \dfrac{1}{3}.\dfrac{3\pi }{2} \right)=\sin \dfrac{\pi }{2}=1$
When ${{x}_{3}}=3\pi ,$ ${{y}_{3}}=\sin \left( \dfrac{1}{3}.3\pi \right)=\sin \pi =0$
When ${{x}_{4}}=\dfrac{9\pi }{2},$ ${{y}_{4}}=\sin \left( \dfrac{1}{3}.\dfrac{9\pi }{2} \right)=\sin \dfrac{3\pi }{2}=-1$
When ${{x}_{5}}=6\pi ,$ ${{y}_{5}}=\sin \left( \dfrac{1}{3}.6\pi \right)=\sin 2\pi =0$
Therefore, the points are $\left( 0,0 \right),\left( \dfrac{3\pi }{2},1 \right),\left( 3\pi ,0 \right),\left( \dfrac{9\pi }{2},-1 \right)$ and $\left( 6\pi ,0 \right)$.
These points are sufficient to draw the graph of the given function.

Note:
The graph of $\sin x$ is very well known to us. It is a periodic function with a period of $2\pi $. The amplitude of this function is 1, that is, the range of the function lies in $\left[ -1,1 \right]$ and the domain of the function is all real numbers, $R$.