Question

How do you graph \[y=\dfrac{3}{4}\] using intercepts?

Answer 1

Hint: To solve this problem, first if all we need to transform the given equation into its intercept form. After doing so, we compare it with the standard intercept form of a straight line. After comparing these two equations or forms, we can find out each intercept. Here, the y-intercept comes out to be \[\dfrac{3}{4}\] and the x-intercept as infinite.

Complete step by step answer:
Every straight line equation can be expressed in the intercept form which is,
\[\dfrac{x}{a}+\dfrac{y}{b}=1\] .... Equation 1
Where, \[a\] is the x-intercept and \[b\] is the y-intercept.
The equation of the straight line given in the question is,
\[y=\dfrac{3}{4}\]
Dividing both sides of the equation by \[\dfrac{3}{4}\] we get,
\[\dfrac{y}{\dfrac{3}{4}}=1\] .... Equation 2
In this equation 1, we find no term involving \[x\]. That means, the coefficient of the x-term is 0. In equation 1, the coefficient of the x-term is \[\dfrac{1}{a}\] . Thus, comparing equation 2 with equation 1, we get
\[\dfrac{1}{a}=0\]
Taking reciprocal on both sides of the equation,
\[a=\dfrac{1}{0}\]
\[a\to \infty \]
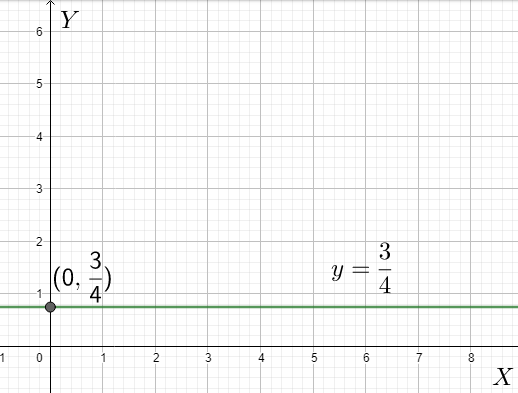
This means that the x-intercept of this line is infinite, or it intersects the x-axis at infinity. In other words, this line is parallel to x-axis. Also, after comparing equation 1 and equation 2 , we see that \[b=\dfrac{3}{4}\]. This means that the y-intercept is \[\dfrac{3}{4}\] .
Therefore, the line will be a line parallel to the x-axis with a y-intercept as \[\dfrac{3}{4}\]. The graph is shown below.

Note:
There is an alternate method to solve this problem. But, this requires us to have complete understanding of straight lines. The line given is
\[y=\dfrac{3}{4}\]
We can clearly see that this is a \[y=c\] line, which means that whatever be the value of \[x\], the corresponding value of \[y\] remains the same. This indicates a line parallel to x-axis. The offset of this line from the x-axis is the constant value of the equation.