Question

How do you graph \[y=\arccos \left( \dfrac{x}{3} \right)\]?

Answer 1

Hint: In order to find the graph of the given equation in the question that is \[y=\arccos \left( \dfrac{x}{3} \right)\], find the points that satisfy this equation and then plot them in the graph.

Complete step by step solution:
Given equation in the question is as follows
\[y=\arccos \left( \dfrac{x}{3} \right)\]
Consider the above equation as the function\[f\left( x \right)=\arccos \left( \dfrac{x}{3} \right)\]
To find the points that satisfy this equation first consider the point at \[x=-3\]
Replace the variable \[x\] with \[-3\]  in the expression, we get:
\[\Rightarrow f\left( -3 \right)=\arccos \left( \dfrac{-3}{3} \right)=\pi \]
\[\Rightarrow f\left( -3 \right)=\pi \]
Now consider the point at \[x=\dfrac{-3}{2}\]
Replace the variable \[x\] with \[\dfrac{-3}{2}\]in the expression, we get:
\[\Rightarrow f\left( \dfrac{-3}{2} \right)=\arccos \left( \dfrac{-\dfrac{3}{2}}{3} \right)\]
Simplify it further and multiply the numerator by the reciprocal of the denominator.
\[\Rightarrow f\left( \dfrac{-3}{2} \right)=\arccos \left( -\dfrac{3}{2}\cdot \dfrac{1}{3} \right)\]
Cancel the common factor of \[3\] to do this follow the following steps:
Move the leading negative in \[\dfrac{-3}{2}\]into the numerator.
\[\Rightarrow f\left( \dfrac{-3}{2} \right)=\arccos \left( -\dfrac{3}{2}\cdot \dfrac{1}{3} \right)\]
Factor \[3\] out of \[-3\].
\[\Rightarrow f\left( -\dfrac{3}{2} \right)=\arccos \left( \dfrac{3\left( -1 \right)}{2}\cdot \dfrac{1}{3} \right)\]
Cancel the common factor.
\[\Rightarrow f\left( -\dfrac{3}{2} \right)=\arccos \left( \dfrac{{3}\cdot -1}{2}\cdot \dfrac{1}{{{3}}} \right)\]
Rewrite the expression, we get:
\[\Rightarrow f\left( -\dfrac{3}{2} \right)=\arccos \left( \dfrac{-1}{2} \right)\]
Move the negative in front of the fraction.
\[\Rightarrow f\left( -\dfrac{3}{2} \right)=\arccos \left( -\dfrac{1}{2} \right)\]
The exact value of \[\arccos \left( -\dfrac{1}{2} \right)\] is \[\dfrac{2\pi }{3}\].
\[\Rightarrow f\left( -\dfrac{3}{2} \right)=\dfrac{2\pi }{3}\]
After this consider the point at \[x=0\]
Replace the variable \[x\] with \[0\] in the expression, we get:
\[\Rightarrow f\left( 0 \right)=\arccos \left( \dfrac{0}{3} \right)\]
Simplify it further and divide \[0\] by \[3\], we get:
\[\Rightarrow f\left( 0 \right)=\arccos \left( 0 \right)\]
The exact value of \[\arccos \left( 0 \right)\] is \[\dfrac{\pi }{2}\].
\[\Rightarrow f\left( 0 \right)=\dfrac{\pi }{2}\]
Now find for the point at \[x=\dfrac{3}{2}\].
Replace the variable \[x\] with \[\dfrac{3}{2}\] in the expression, we get:
\[\Rightarrow f\left( \dfrac{3}{2} \right)=\arccos \left( \dfrac{\dfrac{3}{2}}{3} \right)\]
Simplify it further and multiply the numerator by the reciprocal of the denominator.
\[\Rightarrow f\left( \dfrac{3}{2} \right)=\arccos \left( \dfrac{3}{2}\cdot \dfrac{1}{3} \right)\]
Cancel the common factor of \[3\], we get
\[\Rightarrow f\left( \dfrac{3}{2} \right)=\arccos \left( \dfrac{1}{2} \right)\]
The exact value of \[\arccos \left( \dfrac{1}{2} \right)\]is \[\dfrac{\pi }{3}\].
\[\Rightarrow f\left( \dfrac{3}{2} \right)=\dfrac{\pi }{3}\]
Now at last find the point at \[x=3\]
Replace the variable \[x\]with \[3\] in the expression, we get:
\[\Rightarrow f\left( 3 \right)=\arccos \left( \dfrac{3}{3} \right)\]
Simplify it further and divide \[3\] by \[3\], we get:
\[\Rightarrow f\left( 3 \right)=\arccos \left( 1 \right)\]
The exact value of \[\arccos \left( 1 \right)\]is \[0\].
\[\Rightarrow f\left( 3 \right)=0\]
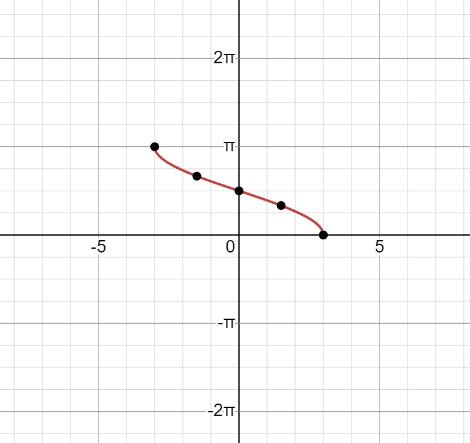
Now list all the points in a table and this trigonometric function can be graphed by plotting these points.
\[\begin{matrix}
   x & f\left( x \right) \\
   -3 & \pi \\
   -\dfrac{3}{2} & \dfrac{2\pi }{3} \\
   0 & \dfrac{\pi }{2} \\
   \dfrac{3}{2} & \dfrac{\pi }{3} \\
   3 & 0 \\
\end{matrix}\]
The graph of the function \[f\left( x \right)=\arccos \left( \dfrac{x}{3} \right)\] is as follows:

Note: Students generally make calculation mistakes while calculating the points that satisfy the graph. It's important to remember the trigonometric values and recheck the calculations once done.