Question

How do you graph $y = {x^2} + 2x$ using a table of values?

Answer 1

Hint: This equation is the quadratic equation. The general form of the quadratic equation is$a{x^2} + bx + c = 0$. Where ‘a’ is the coefficient of ${x^2}$, ‘b’ is the coefficient of x and ‘c’ is the constant term. The graph of the quadratic equation is a parabola. Here, we have to make a function table and select various values of x and plug those values in the given quadratic equation.
The problem with this method is that we might come up with something that does not look like a parabola, a ‘U’ shape. So, to avoid such a problem, we need to start by finding the vertex of the parabola. The formula for vertex is: $\dfrac{{ - b}}{{2a}}$.

Complete step by step solution:
Here, the quadratic equation is
$ \Rightarrow y = {x^2} + 2x$...(1)
Let us compare the above expression with the parabola equation: $y = a{x^2} + bx + c$.
Here, we get the value of ‘a’ is 1, the value of ‘b’ is 2, and the value of ‘c’ is 0.
Let us find the vertex by applying the formula $\dfrac{{ - b}}{{2a}}$.
$ \Rightarrow \dfrac{{ - b}}{{2a}} = \dfrac{{ - 2}}{{2\left( 1 \right)}}$
That is equal to,
$ \Rightarrow \dfrac{{ - b}}{{2a}} = - 1$
Now, substitute the value -1 for x into equation (1).
$ \Rightarrow y = {x^2} + 2x$
$ \Rightarrow y = {\left( { - 1} \right)^2} + 2\left( { - 1} \right)$
That is equal to,
$ \Rightarrow y = 1 - 2$
Therefore,
$ \Rightarrow y = - 1$
So, the vertex of this parabola is located at (-1, -1).
Now, let us try to choose values of x’s that are close to the vertex.
Now, substitute the value -2 for x into equation (1).
$ \Rightarrow y = {x^2} + 2x$
$ \Rightarrow y = {\left( { - 2} \right)^2} + 2\left( { - 2} \right)$
That is equal to,
$ \Rightarrow y = 4 - 4$
Therefore,
$ \Rightarrow y = 0$
So, the vertex of this parabola is located at (-2, 0).
Now, substitute the value 0 for x into equation (1).
$ \Rightarrow y = {x^2} + 2x$
$ \Rightarrow y = {\left( 0 \right)^2} + 2\left( 0 \right)$
That is equal to,
$ \Rightarrow y = 0$
So, the vertex of this parabola is located at (0, 0).
Now, substitute the value 1 for x into equation (1).
$ \Rightarrow y = {x^2} + 2x$
$ \Rightarrow y = {\left( 1 \right)^2} + 2\left( 1 \right)$
That is equal to,
$ \Rightarrow y = 1 + 2$
Therefore,
$ \Rightarrow y = 3$
So, the vertex of this parabola is located at (1, 3).
Now, substitute the value 2 for x into equation (1).
$ \Rightarrow y = {x^2} + 2x$
$ \Rightarrow y = {\left( 2 \right)^2} + 2\left( 2 \right)$
That is equal to,
$ \Rightarrow y = 4 + 4$
Therefore,
$ \Rightarrow y = 8$
So, the vertex of this parabola is located at (2, 8).
Let us substitute these in the graph. This parabola is concave up.

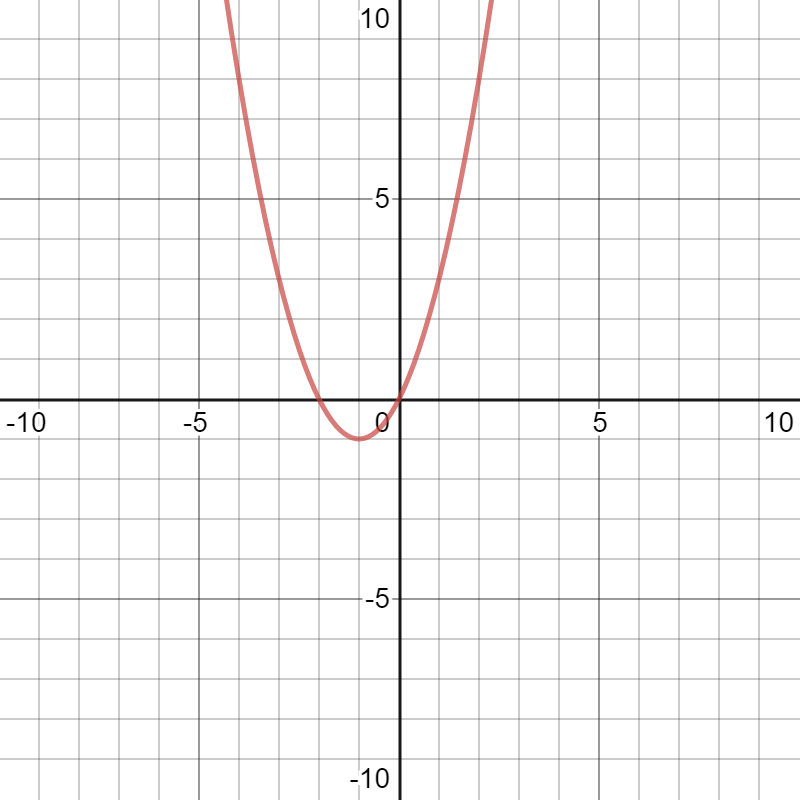
Note:
The x-intercepts are the intersection of the parabola with the x axis which are points on the x-axis and therefore their y coordinates are equal to 0. The y-intercepts are the intersection of the parabola with the x-axis which are points on the y axis and therefore their x coordinates are equal to 0.