
How do you graph $y = \sqrt {x + 1} $, compare it to the parent graph and what is the domain and range?
Answer
558.3k+ views
Hint: Given an expression. We have to plot the graph of the expression and compare it with the parent graph. First, we will determine the parent graph of the function. Now, we will determine the transformation of the function. Then we will determine the domain and range of the function.
Complete step-by-step answer:
We are given the expression $y = \sqrt {x + 1} $.
First, we will determine the parent graph of the function.
$ \Rightarrow y = \sqrt x $
Then, create a table that shows the value of the function for different values of $x$.
Now, we will plot the graph of parent function by plotting the points and joining them.
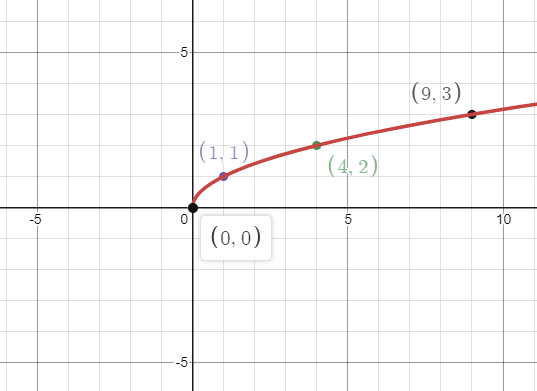
Now, we will determine the expression by moving the graph $y = \sqrt x $ by one unit to the left.
$y = \sqrt {x + 1} $
Now, we will draw the graph of the function $y = \sqrt {x + 1} $ by moving the graph one unit to the left.
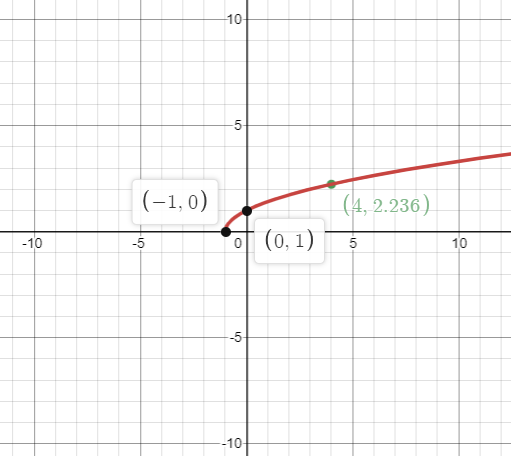
Now, we will determine the domain of the function by equating the radicand to greater than equal to zero.
$ \Rightarrow x + 1 \geqslant 0$
Now, subtract $1$ from both sides, we get:
$ \Rightarrow x + 1 - 1 \geqslant 0 - 1$
$ \Rightarrow x \geqslant - 1$
Therefore, the domain of the function is all real numbers greater than equal to $ - 1$.
Now, we will determine the range of the function which is equal to the output of the function.
Here, the function contains the square root which means the range of the function is the set of all positive numbers greater than or equal to zero.
Hence, the domain of the function is $\left[ { - 1,\infty } \right)$ and range of the function is $\left( { - \infty ,\infty } \right)$.
Note:
In such types of questions the students mainly don't get an approach on how to solve it. In such types of questions students mainly make mistakes while shifting the graph to the left or right. Then, they don’t get an approach on how to calculate the domain of radical expression.
Complete step-by-step answer:
We are given the expression $y = \sqrt {x + 1} $.
First, we will determine the parent graph of the function.
$ \Rightarrow y = \sqrt x $
Then, create a table that shows the value of the function for different values of $x$.
| $x$ | $1$ | $4$ | $9$ |
| $y$ | $1$ | $2$ | $3$ |
Now, we will plot the graph of parent function by plotting the points and joining them.

Now, we will determine the expression by moving the graph $y = \sqrt x $ by one unit to the left.
$y = \sqrt {x + 1} $
Now, we will draw the graph of the function $y = \sqrt {x + 1} $ by moving the graph one unit to the left.

Now, we will determine the domain of the function by equating the radicand to greater than equal to zero.
$ \Rightarrow x + 1 \geqslant 0$
Now, subtract $1$ from both sides, we get:
$ \Rightarrow x + 1 - 1 \geqslant 0 - 1$
$ \Rightarrow x \geqslant - 1$
Therefore, the domain of the function is all real numbers greater than equal to $ - 1$.
Now, we will determine the range of the function which is equal to the output of the function.
Here, the function contains the square root which means the range of the function is the set of all positive numbers greater than or equal to zero.
Hence, the domain of the function is $\left[ { - 1,\infty } \right)$ and range of the function is $\left( { - \infty ,\infty } \right)$.
Note:
In such types of questions the students mainly don't get an approach on how to solve it. In such types of questions students mainly make mistakes while shifting the graph to the left or right. Then, they don’t get an approach on how to calculate the domain of radical expression.
Recently Updated Pages
Master Class 8 Social Science: Engaging Questions & Answers for Success

Master Class 8 English: Engaging Questions & Answers for Success

Class 8 Question and Answer - Your Ultimate Solutions Guide

Master Class 8 Maths: Engaging Questions & Answers for Success

Master Class 8 Science: Engaging Questions & Answers for Success

Master Class 7 English: Engaging Questions & Answers for Success

Trending doubts
Difference Between Plant Cell and Animal Cell

Fill the blanks with the suitable prepositions 1 The class 9 english CBSE

Who is eligible for RTE class 9 social science CBSE

Which places in India experience sunrise first and class 9 social science CBSE

What is pollution? How many types of pollution? Define it

Name 10 Living and Non living things class 9 biology CBSE





