
How do you graph y = $\sec \left( \pi \dfrac{x}{4} \right)$ ?
Answer
540k+ views
Hint: In the given question, we need to graph the function y = $\sec \left( \pi \dfrac{x}{4} \right)$. Secant is the inverse function of cosine, and also helps in finding the values of derived functions. Secant function can be represented as:
$\Rightarrow \sec x=\dfrac{1}{\cos x}$ or $\cos x=\dfrac{1}{\sec x}$
Complete step by step solution:
Let’s discuss the question now.
As we are all aware that cosine is the basic function of trigonometry. Apart from basic functions there are some derived functions too. Secant is also one of the derived functions which is derived from cosine and contributes in deriving other functions. When we say sec $\theta $, here $\theta $ represents angle in either degrees or in radians.
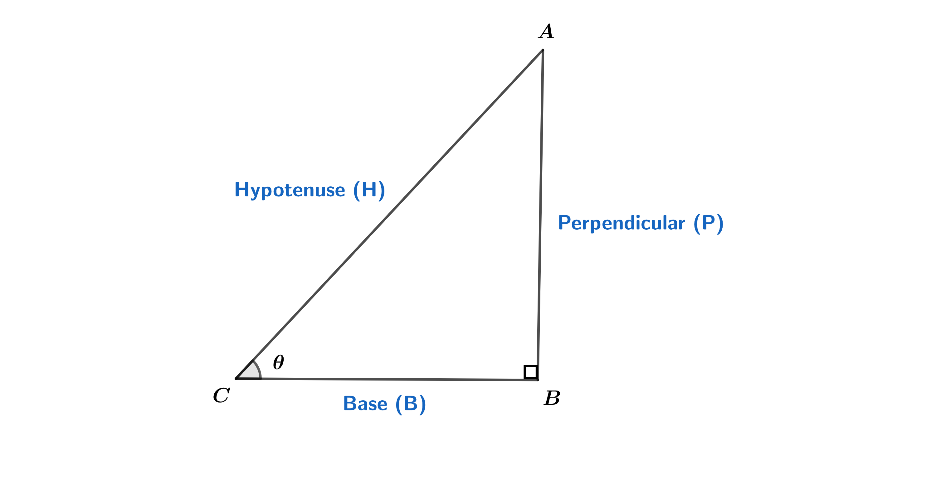
Now, let’s see how we can find the secant value of the angle $\theta $.
In the above triangle, $\theta $ is the angle at C. So,
cos$\theta $ = $\dfrac{base(B)}{hypotenuse(H)}$
Sec$\theta $ is the inverse of cos$\theta $. So we can write it as:
sec$\theta $ = $\dfrac{hypotenuse(H)}{base(B)}$
In this way, we can find the value of the angle given.
Now, next we will move on to some derived functions. They are also called reciprocal identities:
$\Rightarrow $cosec$\theta $ = $\dfrac{1}{\sin \theta }$ or sin$\theta $ = $\dfrac{1}{\cos ec\theta }$
$\Rightarrow $sec$\theta $ = $\dfrac{1}{\cos \theta }$ or cos$\theta $ = $\dfrac{1}{\sec \theta }$
$\Rightarrow $tan$\theta $ = $\dfrac{\sin \theta }{\cos \theta }$ = $\dfrac{1}{\cot \theta }$
$\Rightarrow $cot$\theta $ = $\dfrac{1}{\tan \theta }$ = $\dfrac{\cos \theta }{\sin \theta }$
Now, let’s make table of trigonometric ratios for all the trigonometric functions i.e. sin, cos, tan, cot, sec and cosec.
Finally we just need to plot the graph of y = $\sec \left( \pi \dfrac{x}{4} \right)$.
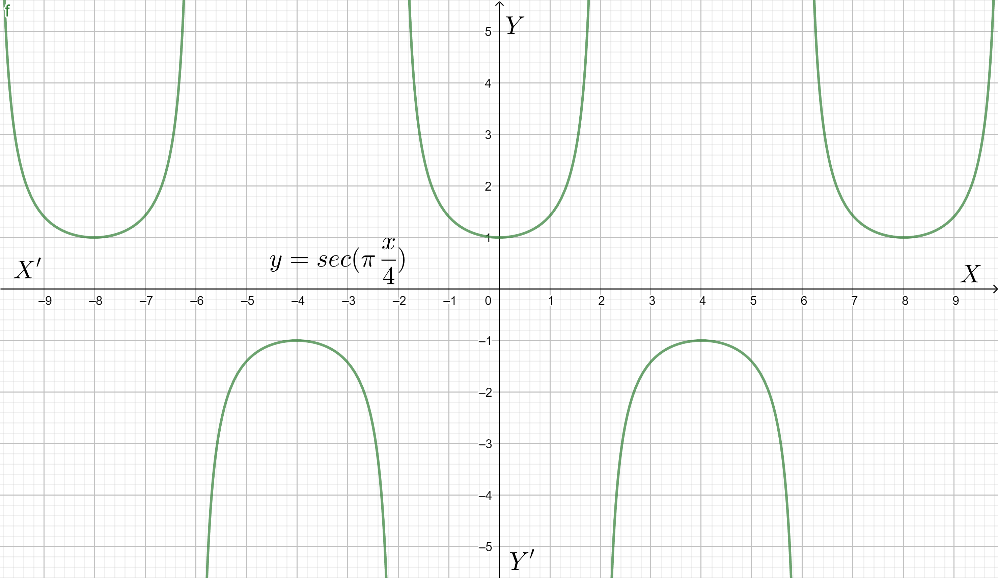
Note: Not only this graph, we can plot any graph of trigonometric function if the angle is given. Trigonometric ratio table is given where different values are given for different angles using six different functions. Those are some common angles that are used everywhere in mathematics that’s why that table is important.
$\Rightarrow \sec x=\dfrac{1}{\cos x}$ or $\cos x=\dfrac{1}{\sec x}$
Complete step by step solution:
Let’s discuss the question now.
As we are all aware that cosine is the basic function of trigonometry. Apart from basic functions there are some derived functions too. Secant is also one of the derived functions which is derived from cosine and contributes in deriving other functions. When we say sec $\theta $, here $\theta $ represents angle in either degrees or in radians.

Now, let’s see how we can find the secant value of the angle $\theta $.
In the above triangle, $\theta $ is the angle at C. So,
cos$\theta $ = $\dfrac{base(B)}{hypotenuse(H)}$
Sec$\theta $ is the inverse of cos$\theta $. So we can write it as:
sec$\theta $ = $\dfrac{hypotenuse(H)}{base(B)}$
In this way, we can find the value of the angle given.
Now, next we will move on to some derived functions. They are also called reciprocal identities:
$\Rightarrow $cosec$\theta $ = $\dfrac{1}{\sin \theta }$ or sin$\theta $ = $\dfrac{1}{\cos ec\theta }$
$\Rightarrow $sec$\theta $ = $\dfrac{1}{\cos \theta }$ or cos$\theta $ = $\dfrac{1}{\sec \theta }$
$\Rightarrow $tan$\theta $ = $\dfrac{\sin \theta }{\cos \theta }$ = $\dfrac{1}{\cot \theta }$
$\Rightarrow $cot$\theta $ = $\dfrac{1}{\tan \theta }$ = $\dfrac{\cos \theta }{\sin \theta }$
Now, let’s make table of trigonometric ratios for all the trigonometric functions i.e. sin, cos, tan, cot, sec and cosec.
| Trigonometric ratios(angle $\theta $ in degrees) | ${{0}^{\circ }}$ | ${{30}^{\circ }}$ | ${{45}^{\circ }}$ | ${{60}^{\circ }}$ | ${{90}^{\circ }}$ |
| sin$\theta $ | 0 | $\dfrac{1}{2}$ | $\dfrac{1}{\sqrt{2}}$ | $\dfrac{\sqrt{3}}{2}$ | 1 |
| cos$\theta $ | 1 | $\dfrac{\sqrt{3}}{2}$ | $\dfrac{1}{\sqrt{2}}$ | $\dfrac{1}{2}$ | 0 |
| tan$\theta $ | 0 | $\dfrac{1}{\sqrt{3}}$ | 1 | $\sqrt{3}$ | $\infty $ |
| cosec$\theta $ | $\infty $ | 2 | $\sqrt{2}$ | $\dfrac{2}{\sqrt{3}}$ | 1 |
| sec$\theta $ | 1 | $\dfrac{2}{\sqrt{3}}$ | $\sqrt{2}$ | 2 | $\infty $ |
| cot$\theta $ | $\infty $ | $\sqrt{3}$ | 1 | $\dfrac{1}{\sqrt{3}}$ | 0 |
Finally we just need to plot the graph of y = $\sec \left( \pi \dfrac{x}{4} \right)$.

Note: Not only this graph, we can plot any graph of trigonometric function if the angle is given. Trigonometric ratio table is given where different values are given for different angles using six different functions. Those are some common angles that are used everywhere in mathematics that’s why that table is important.
Recently Updated Pages
Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Master Class 11 Computer Science: Engaging Questions & Answers for Success

Master Class 11 Social Science: Engaging Questions & Answers for Success

Master Class 11 Maths: Engaging Questions & Answers for Success

Master Class 11 Biology: Engaging Questions & Answers for Success

Trending doubts
Differentiate between an exothermic and an endothermic class 11 chemistry CBSE

One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

Explain zero factorial class 11 maths CBSE

Why is steel more elastic than rubber class 11 physics CBSE

State the laws of reflection of light

What is 1s 2s 2p 3s 3p class 11 chemistry CBSE




