Question

How do you graph $y = \dfrac{8}{{{x^2} - x - 6}}$ using asymptotes, intercepts and end behavior.

Answer 1

Hint: Given an equation of a curve. We have to draw the graph using asymptotes, intercept and end behavior. Horizontal asymptotes are obtained when $y \to \infty $ and vertical asymptotes obtained when $x \to \infty $ .
To find the $x$-intercept of the curve, we substitute $y = 0$ in the equation of the curve as $y$ coordinate is zero on $x$ -axis. Similarly, to find the $y$-intercept of the curve, we substitute $x = 0$ in the equation of the curve as $x$ coordinate is zero on $y$ -axis.
To determine the end behavior of the curve, we substitute $x = \infty $ and $y = \infty $ .

Complete step by step answer:
Step 1:
Given the equation of the curve is $y = \dfrac{8}{{{x^2} - x - 6}}$. The above equation can be written in the form of $\dfrac{{n\left( x \right)}}{{d\left( x \right)}}$ where $n\left( x \right) = 8$ is the numerator of the given curve and $d\left( x \right) = {x^2} - x - 6$ is the denominator of the curve. Now to find the vertical asymptotes, $y \to \infty $ which means, we equate the denominator of the curve to zero, we get
$
  d\left( x \right) = 0 \\
   \Rightarrow {x^2} - x - 6 = 0 \\
 $
Now, factoring the above equation, we get
$
   \Rightarrow {x^2} - 3x + 2x - 6 = 0 \\
   \Rightarrow x\left( {x - 3} \right) + 2\left( {x - 3} \right) = 0 \\
   \Rightarrow \left( {x - 3} \right)\left( {x + 2} \right) = 0 \\
 $
Equating $x - 3 = 0$, we get $x = 3$ and equating $x + 2 = 0$ , we get $x = - 2$ . So vertical asymptotes of the curve is $x = 3$ and $x = - 2$ .

Step 2:
To determine the horizontal asymptotes, as $x \to \infty $. we get
 \[
  y = \dfrac{8}{{{{\left( \infty \right)}^2} - \left( \infty \right) - 6}} \\
  y = \dfrac{8}{\infty } \\
  y = 0 \\
 \]
So the horizontal asymptote of the curve is at $y = 0$.

Step 3:
Now to find $x$ intercept of the curve, we substitute $y = 0$ in the equation of the curve, then we get
\[
  0 = \dfrac{8}{{{x^2} - x - 6}} \\
   \Rightarrow 8 = 0 \\
 \]
This is not true so the$x$ intercept of the curve does not lie.

Step 4:
To determine $y$ intercept of the curve, we substitute $y = 0$ in the equation of the curve, then we get
\[
  y = \dfrac{8}{{{{\left( 0 \right)}^2} - \left( 0 \right) - 6}} \\
   \Rightarrow y = - \dfrac{4}{3} \\
 \]
So, $y$ intercept of the curve is at $\left( {0, - \dfrac{4}{3}} \right)$.

Step 5:
Now as $x \to \infty $ the value of $y = \dfrac{8}{{{{\left( \infty \right)}^2} - \left( \infty \right) - 6}} = 0$ .
Also as $x \to - \infty $ the value of $y = \dfrac{8}{{{{\left( { - \infty } \right)}^2} - \left( { - \infty } \right) - 6}} = 0$ .
This means as $x$ approaches towards infinity, the curve touches the $x$ axis.

Step 6:
Now we draw the graph of the curve. From the above steps, it is clear that the $x$ intercept of the curve does not lie and the $y$ intercept of the curve is at $\left( {0, - \dfrac{4}{3}} \right)$ .
Horizontal asymptote is at $y = 0$ and vertical asymptotes are at $x = 3$ and $x = - 2$ .
Below is the graph of the curve

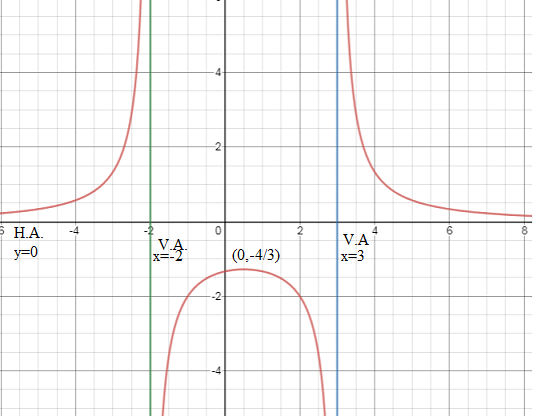
Note: Asymptotes of the curve is a line such that the distance between the line and curve approaches towards zero as one or both of the $x$ or $y$ coordinates tends to infinity.
In the middle term splitting method, split the middle term such that the addition of both terms is equal to the middle term and the product of both terms is equal to the product of the first and last term.