Question

How do you graph $y = 5x - \dfrac{5}{2}$ using slopes and intercepts.

Answer 1

Hint: We will first write the general equation of a line and then compare it with the given to find the slope and intercepts. Then, we will use those to form the graph.

Complete step-by-step solution:
We are given that we are required to graph the equation given by $y = 5x - \dfrac{5}{2}$ using slopes and intercepts.
The general equation of a line is given by y = mx + c, where m is the slope of the line.
Now, we are given the line $y = 5x - \dfrac{5}{2}$. If we compare this to the above mentioned line, we will then obtain: m = 5 and c = - 5/2.
Therefore, the slope of the given line is 5.
Now, we need to find the intercepts. Let us put in x = 0 in the equation $y = 5x - \dfrac{5}{2}$ to find the y – intercept.
Putting x = 0 in $y = 5x - \dfrac{5}{2}$ , we will get y = - 5/2.
So, the y – intercept of the given line is – 5/2.
Let us put in y = 0 in the equation $y = 5x - \dfrac{5}{2}$ to find the x – intercept.
Putting y = 0 in $y = 5x - \dfrac{5}{2}$ , we will get x = 1/2.
So, the x – intercept of the given line is 1/2.
Now, since the slope is positive, therefore, the line makes the angle of less than 90 degrees or more than 180 and less than 270 degrees with the positive direction of x – axis. Now, we also have both the x and y intercepts, so plotting those two points and joining them to form the line, we will then obtain the following graph:-

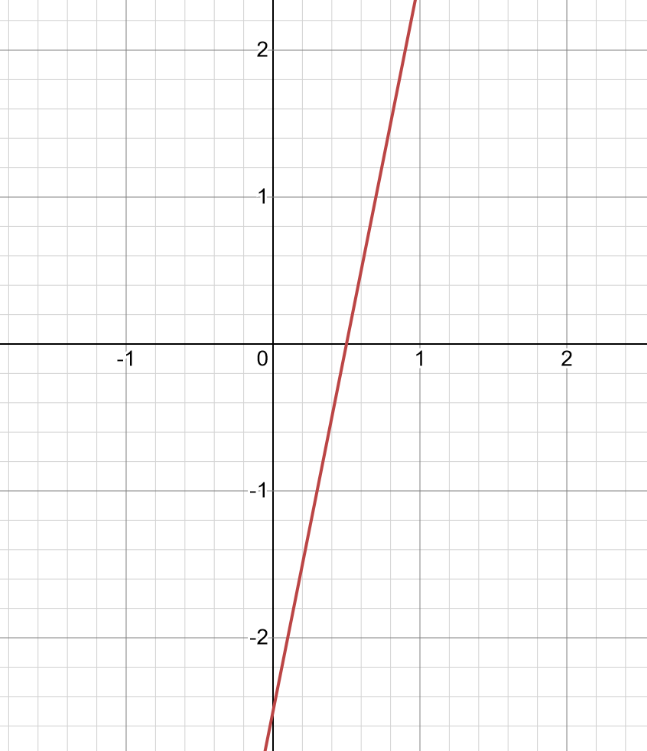
Note: The students must note that the x and y intercepts basically refer to the points where the line cuts the x – axis and y – axis at. The point where coordinate axis cut the line at x – axis is x – intercept and y – axis is y – intercept.
The students must also know that the slope of a line is basically the tangent of the angle the line makes with the positive x – axis. Here, in this question, we have tangent of the angle the given line is making with the positive x – axis as 5.