Question

How do you graph $y = 2x - 1$by plotting points ?

Answer 1

Hint:
Since this is a graphical numerical, the student has to find the coordinates by substituting either $x$ or $y$ or both as $0$. The first step in solving the sum is to analyze the equation of the curve and figure out which curve it is, i.e. a circle, parabola, or a line. From the given equation we can see that it is an equation of a line. To plot the line on a graph, a student has to mark $2$points on the graph. For the first point he has to substitute $x = 0$ & for the second point substituting $y = 0$. Once the student has $2$ points, he can join the points to form the line. Also just to make sure the plotting has been done correctly, students have to find the third point by putting$x = 1$. Thus after plotting if all the points lie on the same line then we can say plotting has been done correctly.

Complete Step by Step Solution:
Let's start plotting points one after the other. First point can be plotted after substituting $x = 0$.
So the equation becomes$y = - 1$.
Therefore, the first point is $(0, - 1)...........(1)$
In order to find the second point, let us substitute $y = 0$.
So the coordinate of Point $x$is $\dfrac{1}{2}$.
Second Point is $(\dfrac{1}{2},0$)
Since we have two coordinates we can plot a line on the graph paper.
To make sure that our points are correct we need to plot the third point by substituting $x = 1$.
Third point becomes $(1,1)$.

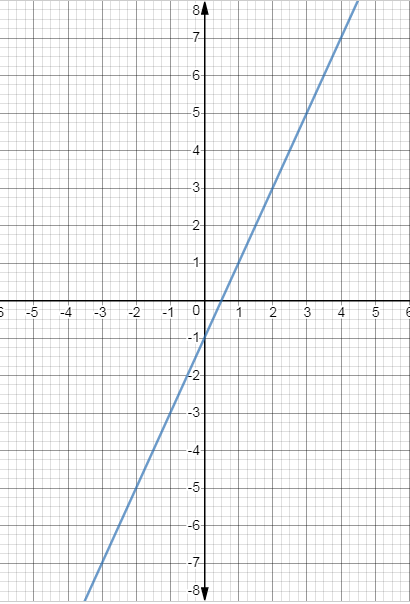
Since all the points lie on the same plane, we can say that the coordinates are proper and we have plotted the line correctly on the graph

Note:
Since this is a graphical sum, the student should always cross-check his/her answer by picking up any point from the $x - axis$ and substituting its value in the equation. If the value of the $y$ obtained is the same as that on the graph, he can say that the line is plotted correctly. It is always necessary to cross-check as the student may go wrong while substituting values for a complex curve like a parabola, hyperbola, or a circle. So if the student verifies his answer by this method he will never go wrong.