
How do you graph $ y = 2\sin \left( {2x + \dfrac{\pi }{2}} \right) + 3 $ ?
Answer
528.3k+ views
Hint: A graph of a function f is the set of ordered pairs; the equation of the graph is generally represented as $ y = f\left( x \right) $ , where x and $ f\left( x \right) $ are real numbers. We substitute the value of x and we determine the value of y and then we mark the points in the graph and we join the points.
Complete step by step solution:
Here, in the given question, we have to plot the graph for the given function. The values of x and y that satisfy the given function are known as the solutions. These pairs are in the form of cartesian coordinates.
First, we have to find the value of y by using the graph equation $ y = 2\sin \left( {2x + \dfrac{\pi }{2}} \right) + 3 $ .
Let us substitute the value of x as $ 0 $ .
$ \Rightarrow y = 2\sin \left( {2\left( 0 \right) + \dfrac{\pi }{2}} \right) + 3 $
$ \Rightarrow y = 2\sin \left( {\dfrac{\pi }{2}} \right) + 3 $
Now, we know that the value of $ \sin \left( {\dfrac{\pi }{2}} \right) $ is $ 1 $ .
$ \Rightarrow y = 2 + 3 $
$ \Rightarrow y = 5 $
Now we consider the value of x as $ \dfrac{\pi }{2} $ , the value of y is
$ \Rightarrow y = 2\sin \left( {2\left( {\dfrac{\pi }{2}} \right) + \dfrac{\pi }{2}} \right) + 3 $
$ \Rightarrow y = 2\sin \left( {\pi + \dfrac{\pi }{2}} \right) + 3 $
We know that the value of $ \sin \left( {\dfrac{{3\pi }}{2}} \right) $ is $ - 1 $ .
$ \Rightarrow y = 2\left( { - 1} \right) + 3 $
$ \Rightarrow y = 1 $
Now we consider the value of x as $ \pi $ , the value of y is
$ \Rightarrow y = 2\sin \left( {2\pi + \dfrac{\pi }{2}} \right) + 3 $
$ \Rightarrow y = 2\sin \left( {\dfrac{{5\pi }}{2}} \right) + 3 $
We know that $ \sin \left( {\dfrac{{5\pi }}{2}} \right) $ is equal to $ 1 $ . So, we get,
$ \Rightarrow y = 2\left( 1 \right) + 3 $
$ \Rightarrow y = 5 $
Now we consider the value of x as $ \dfrac{\pi }{4} $ , the value of y is
$ \Rightarrow y = 2\sin \left( {2\left( {\dfrac{\pi }{4}} \right) + \dfrac{\pi }{2}} \right) + 3 $
$ \Rightarrow y = 2\sin \left( {\dfrac{\pi }{2} + \dfrac{\pi }{2}} \right) + 3 $
$ \Rightarrow y = 2\sin \left( \pi \right) + 3 $
Value of $ \sin \left( \pi \right) $ is zero. So, we get,
$ \Rightarrow y = 2\left( 0 \right) + 3 $
$ \Rightarrow y = 3 $
Now, we draw a table for these values we have
We also know the nature of the graph of sine function. Hence, we can now plot the graph of the given function $ y = 2\sin \left( {2x + \dfrac{\pi }{2}} \right) + 3 $ . The graph plotted for these points is represented below:
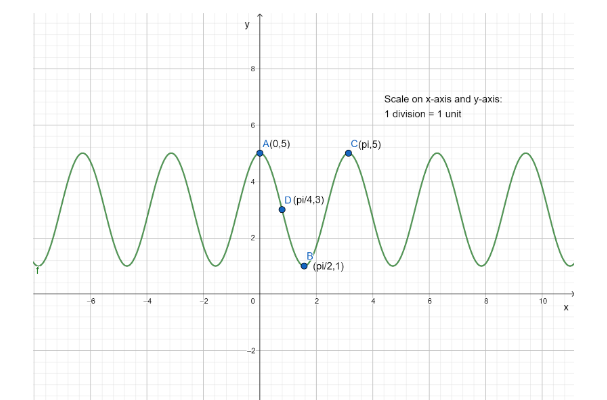
Note: The sine function can be represented by the general equation $ y = a\sin \left( {kx + \phi } \right) $ . There are various parameters in this equation such as the amplitude, period and phase shift of the sine function. The value ‘a’ is the amplitude of the sine function $ y = a\sin \left( {kx + \phi } \right) $ . The period of the sine function can be calculated as $ \left( {\dfrac{{2\pi }}{k}} \right) $ as the value of the function repeats after regular interval of $ \left( {\dfrac{{2\pi }}{k}} \right) $ radians. Also, if there is a constant added in the function like $ y = a\sin \left( {kx + \phi } \right) + p $ , then the graph of the function moves p units vertically upwards due to the upward shift.
Complete step by step solution:
Here, in the given question, we have to plot the graph for the given function. The values of x and y that satisfy the given function are known as the solutions. These pairs are in the form of cartesian coordinates.
First, we have to find the value of y by using the graph equation $ y = 2\sin \left( {2x + \dfrac{\pi }{2}} \right) + 3 $ .
Let us substitute the value of x as $ 0 $ .
$ \Rightarrow y = 2\sin \left( {2\left( 0 \right) + \dfrac{\pi }{2}} \right) + 3 $
$ \Rightarrow y = 2\sin \left( {\dfrac{\pi }{2}} \right) + 3 $
Now, we know that the value of $ \sin \left( {\dfrac{\pi }{2}} \right) $ is $ 1 $ .
$ \Rightarrow y = 2 + 3 $
$ \Rightarrow y = 5 $
Now we consider the value of x as $ \dfrac{\pi }{2} $ , the value of y is
$ \Rightarrow y = 2\sin \left( {2\left( {\dfrac{\pi }{2}} \right) + \dfrac{\pi }{2}} \right) + 3 $
$ \Rightarrow y = 2\sin \left( {\pi + \dfrac{\pi }{2}} \right) + 3 $
We know that the value of $ \sin \left( {\dfrac{{3\pi }}{2}} \right) $ is $ - 1 $ .
$ \Rightarrow y = 2\left( { - 1} \right) + 3 $
$ \Rightarrow y = 1 $
Now we consider the value of x as $ \pi $ , the value of y is
$ \Rightarrow y = 2\sin \left( {2\pi + \dfrac{\pi }{2}} \right) + 3 $
$ \Rightarrow y = 2\sin \left( {\dfrac{{5\pi }}{2}} \right) + 3 $
We know that $ \sin \left( {\dfrac{{5\pi }}{2}} \right) $ is equal to $ 1 $ . So, we get,
$ \Rightarrow y = 2\left( 1 \right) + 3 $
$ \Rightarrow y = 5 $
Now we consider the value of x as $ \dfrac{\pi }{4} $ , the value of y is
$ \Rightarrow y = 2\sin \left( {2\left( {\dfrac{\pi }{4}} \right) + \dfrac{\pi }{2}} \right) + 3 $
$ \Rightarrow y = 2\sin \left( {\dfrac{\pi }{2} + \dfrac{\pi }{2}} \right) + 3 $
$ \Rightarrow y = 2\sin \left( \pi \right) + 3 $
Value of $ \sin \left( \pi \right) $ is zero. So, we get,
$ \Rightarrow y = 2\left( 0 \right) + 3 $
$ \Rightarrow y = 3 $
Now, we draw a table for these values we have
| X | $ 0 $ | $ \dfrac{\pi }{2} $ | $ \pi $ | $ \dfrac{\pi }{4} $ |
| y | $ 5 $ | $ 1 $ | $ 5 $ | $ 3 $ |
We also know the nature of the graph of sine function. Hence, we can now plot the graph of the given function $ y = 2\sin \left( {2x + \dfrac{\pi }{2}} \right) + 3 $ . The graph plotted for these points is represented below:

Note: The sine function can be represented by the general equation $ y = a\sin \left( {kx + \phi } \right) $ . There are various parameters in this equation such as the amplitude, period and phase shift of the sine function. The value ‘a’ is the amplitude of the sine function $ y = a\sin \left( {kx + \phi } \right) $ . The period of the sine function can be calculated as $ \left( {\dfrac{{2\pi }}{k}} \right) $ as the value of the function repeats after regular interval of $ \left( {\dfrac{{2\pi }}{k}} \right) $ radians. Also, if there is a constant added in the function like $ y = a\sin \left( {kx + \phi } \right) + p $ , then the graph of the function moves p units vertically upwards due to the upward shift.
Recently Updated Pages
Master Class 11 Computer Science: Engaging Questions & Answers for Success

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Master Class 11 Maths: Engaging Questions & Answers for Success

Master Class 11 Biology: Engaging Questions & Answers for Success

Trending doubts
One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

There are 720 permutations of the digits 1 2 3 4 5 class 11 maths CBSE

Discuss the various forms of bacteria class 11 biology CBSE

Draw a diagram of a plant cell and label at least eight class 11 biology CBSE

State the laws of reflection of light

Explain zero factorial class 11 maths CBSE




