Question

How do you graph \[y - 2 = \dfrac{2}{3}\left( {x - 4} \right)\]?

Answer 1

Hint:
The easiest way to find points on the line of the given equation \[y - 2 = \dfrac{2}{3}\left( {x - 4} \right)\] is to convert the given equation in point slope form to slope intercept form: \[y = mx + b\], where m is the slope, and b is the y-intercept. In order to do this, solve the point slope equation for y, then consider any x values to graph the solution.

Complete step by step solution:
Let us write the given equation:
 \[y - 2 = \dfrac{2}{3}\left( {x - 4} \right)\]
Every straight line can be represented by an equation \[y = mx + b\], hence let us apply the slope intercept form to graph the solution.
\[y - 2 = \dfrac{2}{3}\left( {x - 4} \right)\]
Add 2 on both sides of the given equation as:
\[y - 2 + 2 = \dfrac{2}{3}\left( {x - 4} \right) + 2\]
\[ \Rightarrow \]\[y = \dfrac{2}{3}\left( {x - 4} \right) + 2\]
Now let us simplify the obtain equation
\[\dfrac{2}{3}\left( {x - 4} \right) + 2\] to \[\dfrac{{2\left( {x - 4} \right)}}{3}\]
\[ \Rightarrow \]\[y = \dfrac{{2\left( {x - 4} \right)}}{3} + 2\]
Expand the terms as:
\[y = \dfrac{{2x}}{3} - \dfrac{8}{3} + 2\]
Now simplify the terms
\[y = \dfrac{2}{3}x - \dfrac{8}{3} + 2\]
Multiply 2 by \[\dfrac{3}{3}\] to get the same denominator as \[ - \dfrac{8}{3}\] i.e.,
\[y = \dfrac{2}{3}x - \dfrac{8}{3} + 2 \times \dfrac{3}{3}\]
Simplifying the terms, we get
\[y = \dfrac{2}{3}x - \dfrac{8}{3} + \dfrac{6}{3}\]
\[y = \dfrac{2}{3}x - \dfrac{2}{3}\] ……….. 1
Determine two or three points on the line by choosing values for x and solving for y.
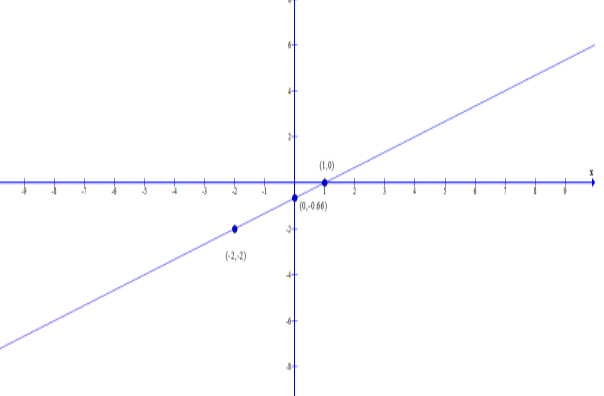
Let us consider the points at x as -2, 0 and 1.
Substitute the values of x in equation 1, hence we get
\[x = - 2,y = - 2\]
\[x = 0,y = - \dfrac{2}{3}\]or 0.66
\[x = 1,y = 0\]
Now, let us graph the solution at \[x = - 2,y = - 2\],
\[x = 0,y = - \dfrac{2}{3}\] and \[x = 1,y = 0\]
Plot the points and draw a straight line through them.

Note:
In slope intercept form; very often, linear-equation word problems deal with changes over the course of time i.e., \[y = mx + b\] the number b is the coordinate on the y-axis where the graph crosses the y-axis and also, we can solve the given equation using intercept form i.e., when x = 0, the corresponding y-value is the y-intercept. In the particular context of word problems, the y-intercept (that is, the point when x = 0) also refers to the starting value.