Question

How do you graph \[{x^2} + {y^2} - 6x + 8y + 9 = 0\] ?

Answer 1

Hint: We need to know the standard form of a circle equation to solve this question. This question involves the arithmetic operations like addition/ subtraction/ multiplication/ division. Also, we need to know the basic algebraic formulae to make an easy calculation. We need to know how to draw a graph with the help of a given equation.

Complete step by step solution:
The given equation is shown below,
 \[{x^2} + {y^2} - 6x + 8y + 9 = 0 \to \left( 1 \right)\]
We know that,
The standard form of circle equation is,
 \[{\left( {x - a} \right)^2} + {\left( {y - b} \right)^2} = {r^2} \to \left( 2 \right)\]
Here, \[\left( {a,b} \right)\] is the centre of the circle,
And \[r\] is the radius of the circle.
We would convert the equation \[\left( 1 \right)\] into the form of the equation \[\left( 2 \right)\] . So, let’s rearrange the equation \[\left( 1 \right)\] , as given below,
 \[{x^2} - 6x + {y^2} + 8y = - 9 \to \left( 3 \right)\]
( \[6x\] Can be written as \[2 \times 3 \times x\]
 \[8y\] Can be written as \[2 \times 4 \times y\] )
Let’s add \[{3^2}\] and \[{4^2}\] on both sides of the equation \[\left( 3 \right)\] , we get
 \[{x^2} - 6x + {3^2} + {y^2} + 8y + {4^2} = - 9 + {3^2} + {4^2} \to \left( 4 \right)\]
We know that,
 \[{\left( {a + b} \right)^2} = {a^2} + {b^2} + 2ab\] And
 \[{\left( {a - b} \right)^2} = {a^2} + {b^2} - 2ab\]
By using the above two algebraic formula, we get
 \[{x^2} - 6x + {3^2} = {\left( {x - 3} \right)^2}\] And
 \[{y^2} + 2y + {4^2} = {\left( {y + 4} \right)^2}\]
Let’s substitute the above two equations in the equation \[\left( 4 \right)\] , we get
 \[\left( 4 \right) \to {x^2} - 6x + {3^2} + {y^2} + 8y + {4^2} = - 9 + {3^2} + {4^2}\]
 \[{\left( {x - 3} \right)^2} + {\left( {y + 4} \right)^2} = - 9 + 9 + {4^2}\]
So, we get
 \[{\left( {x - 3} \right)^2} + {\left( {y + 4} \right)^2} = {4^2} \to \left( 5 \right)\]
Let’s compare the equation \[\left( 2 \right)\] and \[\left( 5 \right)\] , we get
 \[\left( 2 \right) \to {\left( {x - a} \right)^2} + {\left( {y - b} \right)^2} = {r^2}\]
 \[\left( 5 \right) \to {\left( {x - 3} \right)^2} + {\left( {y + 4} \right)^2} = {4^2}\]
So, we get \[a = 3,b = - 4\] and \[r = 4\]
So, the centre \[\left( {a,b} \right) = \left( {3, - 4} \right)\] and the radius \[r = 4\]
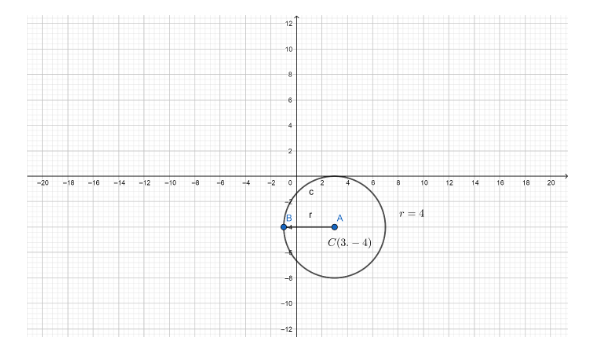
By using the above information we can draw the following graph,
The above graph has defined the equation,
 \[{x^2} + {y^2} - 6x + 8y + 9 = 0\]

Note: Remember the standard form of the circle equation. Also, note that for making the given equation to algebraic formulae we can add/ subtract/ multiply/ divide any number with the equation into both sides. Also, note that in the equation \[{\left( {x - a} \right)^2} + {\left( {y - b} \right)^2} = {r^2}\] , the centre of the circle is mentioned as \[\left( {a,b} \right)\] and the radius of the circle is mentioned as \[r\] .