Question

How do you graph ${{x}^{2}}+{{y}^{2}}=9$ and what are its lines of symmetry? \[\]

Answer 1

Hint: We recall the definition of lines of symmetry and circle. We recall that the standard equation of circle in centre-radius form with centre $\left( a,b \right)$ and radius $r$ is given by ${{\left( x-a \right)}^{2}}+{{\left( y-b \right)}^{2}}={{r}^{2}}$. We compare the standard equation with the given equation and find the centre and radius of the given circle to plot it. We find the lines symmetry as the lines which bisect the circles into two semi-circle. \[\]

Complete step by step answer:
We know in mirror symmetry or reflection symmetry is symmetry where the shape of an object does not change after reflection. A line of symmetry exists at equal distance from object and image. Hence a line of symmetry for any object will divide the object into two equal shapes which are mirror reflection of each other. \[\]
We know that equation of a circle the centre-radius form can between with coordinates of centre $\left( a,b \right)$ and length of the radius $r$ as
\[{{\left( x-a \right)}^{2}}+{{\left( y-b \right)}^{2}}={{r}^{2}}\]
We are given the following implicit equation in the question
\[{{x}^{2}}+{{y}^{2}}={{9}^{2}}\]
We observe the above equation and standard equation of circle in centre-radius and find that they are quite similar. We can write the above equation as
\[{{\left( x-0 \right)}^{2}}+{{\left( y-0 \right)}^{2}}={{3}^{2}}\]
We now again compare the above equation and standard equation of circle in centre-radius to find centre as $\left( a,b \right)=\left( 0,0 \right)$ and radius as $r=3$. So we draw the circle with centre at origin $\left( 0,0 \right)$ and radius $r=3$.

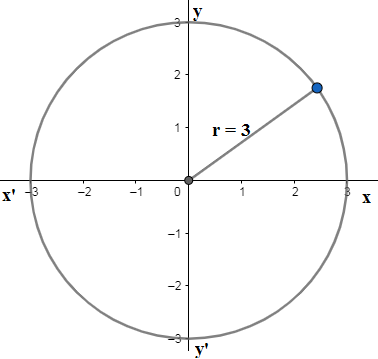
The line of symmetries will divide the circle into two congruent halves which means semicircle with radius $r=3$. So that line will be passing through the centre and hence lines of symmetry of the circle are its diameters. Here $x-$axis and $y-$axis are among the lines of symmetry. \[\]

Note: We note that we call alternatively plot the given implicit equation ${{x}^{2}}+{{y}^{2}}=9$ by converting it to implicit equation $y=\pm \sqrt{9-{{x}^{2}}}$ where $y=\sqrt{9-{{x}^{2}}}$ will represent the semi-circle above $x-$axis and $y=-\sqrt{9-{{x}^{2}}}$ will represent the semi-circle below $x-$axis. The form of the circle is a quadratic equation form which is ${{x}^{2}}+{{y}^{2}}+2gx+2fy+c=0$.