Question

How do you graph $x+5y=5$ using intercepts? \[\]

Answer 1

Hint: We recall the definition of intercepts as non-zero coordinates of points of intersection, say $\left( a,0 \right),\left( 0,b \right)$of the line with the axes. We use satisfaction of these points of the line to find the intercepts and then the points. We join two points on the axes to find the graph of $x+5y=5$. \[\]

Complete answer:
We know that we need at least two points to draw a line. We also know that every linear equation $Ax+By+C=0$ can be represented as a line in the $xy-$plane. If the line cuts the $y-$axis at the point $\left( 0,b \right)$ and cuts the $x-$axis at the point $\left( a,0 \right)$ then $b$ is called the $y-$intercept and $a$ is called $x-$intercept of the line.
We are given the following equation in the question
\[x+5y=5\]
Let the given line cut the $y-$axis at $\left( 0,b \right)$. So by satisfaction of the coordinates we have the $y-$intercept as
 \[\begin{align}
  & 0+5\cdot b=5 \\
 & \Rightarrow 5b=5 \\
 & \Rightarrow b=1 \\
\end{align}\]
Let the given line cut the $x-$axis at the point$\left( a,0 \right)$. So by satisfaction of the coordinates we have the $x-$intercept as
\[\begin{align}
  & a+5\cdot 0=5 \\
 & \Rightarrow a=5 \\
\end{align}\]
 So we have got two points $\left( a,0 \right)=\left( 5,0 \right),\left( 0,b \right)=\left( 0,1 \right)$. We can join them to find the decreasing line in a graph paper. \[\]

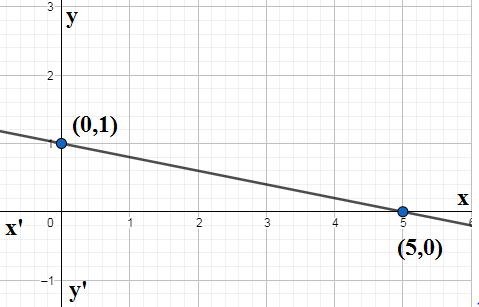
Note: We note that the standard form or the intercept of the equation is given by $Ax+By=C$from which we can directly find the $x-$intercept as $\dfrac{-C}{A}$ and the $y-$intercept as $\dfrac{-C}{B}$. If both the intercepts are positive or negative we get a decreasing line from left to right. If only one of the intercept is positive we get an increasing line from left to right. If $C=0$ we get a line passing through origin. The other form of equation line is slope-point form which is given by $y=mx+c$.