Question

How do you graph $x+3y=6$ using intercepts?

Answer 1

Hint: We will look at the definition of an intercept. Then we will find the x-intercept and the y-intercept from the given equation. We will use the interpretation of these intercepts to plot the graph of the given equation. We will verify that the type of given equation and its representation as a graph are correct.

Complete step by step answer:
We define the intercept to be the point where the line intersects either axes on the cartesian plane. So, the x-intercept is the point at which the line intersects the x-axis. Similarly, the y-intercept is the point at which the line intersects the y-axis. Since the x-intercept is the intersection of the line with the x-axis, we can find it by substituting $y=0$ in the equation of the line. The given equation is $x+3y=6$. Now, substituting $y=0$ in this equation we get
$\begin{align}
  & x+3\left( 0 \right)=6 \\
 & \therefore x=6 \\
\end{align}$
The x-intercept is $\left( 6,0 \right)$. Similarly, we will find the y-intercept. The y-intercept is the intersection of the line with the y-axis. So, we can find it by substituting $x=0$ in the equation of the line. Therefore, substituting $x=0$ in this equation we get
$\begin{align}
  & 0+3y=6 \\
 & \Rightarrow 3y=6 \\
 & \therefore y=2 \\
\end{align}$
So, the y-intercept is $\left( 0,2 \right)$. Now, according to the definition of the intercept, we know that the line represented by the given equation passes through the x-intercept and the y-intercept, which are the points $\left( 6,0 \right)$ and $\left( 0,2 \right)$. The given equation is a linear equation. We know that only one line passes through two points. So, we can draw the graph of the given equation as a line passing through the x-intercept and y-intercept.

The graph looks like the following,

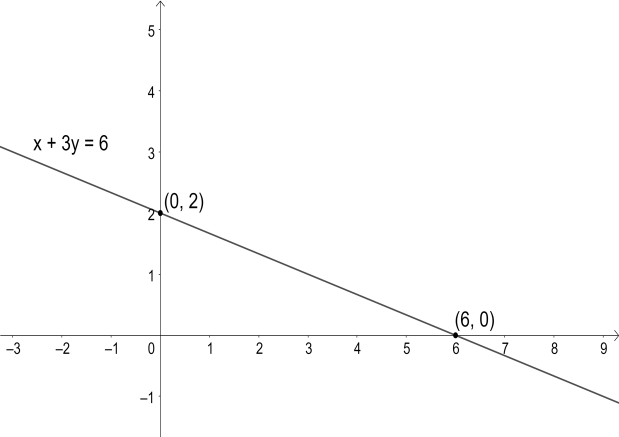
The linear equation represents a graph of a straight line, which is as expected.


Note: The graph of a linear equation is a line. The graph of a quadratic equation is a parabola. By analyzing the equation given, we can infer certain details about the graph it represents. These details include intercepts or vertices of a parabola representing a quadratic equation. It is important to understand these concepts so that solving equations and interpreting them becomes intuitive.