Question

How do you graph using the intercepts for \[4x + y = - 21\] ?

Answer 1

Hint: In order to graph plot for the equation, \[4x + y = - 21\] , we need the points to be plotted in the graph, however here, we need to draw using the intercepts , for this, we can find the two intercepts , \[x - \] and \[y - \] intercepts by putting \[x\] and \[y\] zero one by one and then simply plotting the intercepts.

Complete step-by-step answer:
The formula used for the graph is for finding the intercepts. For finding \[x - \] intercept, first put \[y = 0\] in the equation and in order to find the \[y - \] intercept, put \[x = 0\] , in this way the two points for the graph are found and then plotted to get a straight line graph.

Firstly let us write the equation, for which we need to plot the graph
 \[4x + y = - 21\]
Let us find the \[x - \] and \[y - \] intercepts
Now, to find the \[x - \] intercept, put \[y = 0\] in the equation
i.e.
  $
  4x + y = - 21 \\
   \Rightarrow 4x + 0 = - 21 \\
   \Rightarrow 4x = - 21 \\
   \Rightarrow x = \dfrac{{ - 21}}{4} \;
 $
Therefore, the \[x - \] intercept is \[\dfrac{{ - 21}}{4}\]
Now, let us find the \[y - \] intercept
For this, let us put \[x = 0\] in the equation
 $
  4x + y = - 21 \\
   \Rightarrow 4\left( 0 \right) + y = - 21 \\
   \Rightarrow y = - 21 \;
 $
Thus, we get the \[y - \] intercept, which is \[ - 21\]
Therefore, we get the intercept points as
 \[\left( {\dfrac{{ - 21}}{4},0} \right)\] and \[\left( {0, - 21} \right)\]
Now, if we plot these two points in the graph, we get

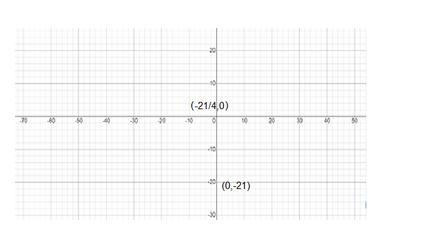
Now, this equation is for a straight line graph for which the intercepts have been drawn
If we join the two points, we get the graph as required

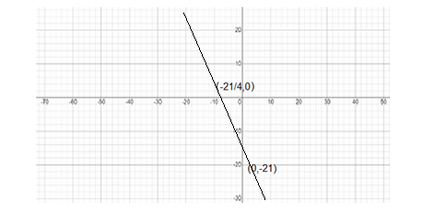
Hence, the graph is plotted.

Note: Alternatively, this can also be solved by looking at the equation
 $
4x + y = - 21 \\
  y = - 4x - 21 \;
 $
This equation is of the form \[y = mx + c\]
Where, \[m\] is the slope and \[c\] is the \[y - \] intercept,
And \[x - \] intercept is found in the same way as before.