Question

How do you graph using slope and intercept of $4x + y = 4$.

Answer 1

Hint: Here we need to draw a graph and find intercepts and slope for the given equation. The equation of any straight line, called a linear equation, can be written as : y =mx + b, where m is the slope of the line and b is the y-intercept. The x-intercept is where a line crosses the x-axis and y-intercept is the point where the line crosses the y-axis. The slope of a line is a number that describes both direction and the steepness of the line. It can be calculated by change in y-value by change in x-value. We need to convert the given equation in slope intercept form and then find the values of y by assuming x values and then we represent the intercepts in a graph.

Complete step-by-step solution:
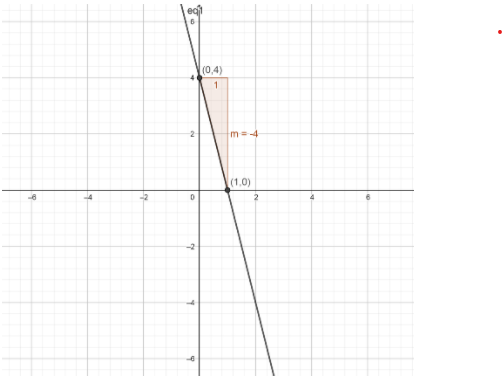
Consider the equation $4x + y = 4$
Now we need to convert this equation in slope intercept form of
$y = mx + b$
Then$4x + y = 4$ becomes
$y = 4 - 4x - - - - - - - - (1)$
By comparing equation of straight line, we find slope
Here the coefficient of x is slope,
$m = - 4$
Now substituting when $x = 0$in equation (1), we get
$y = 4 - 4(0)$
$y = 4$
Now substituting when $x = 1,$ in equation (1), we get
$y = 4 - 4(1)$
$y = 0$
Therefore the intercepts are \[\left( {0,4} \right)\] and \[\left( {1,0} \right)\]

Note: In maths, a graph can be defined as a pictorial representation or a diagram that represents data or values in an organised manner.
The point on the graph often represents the relationship between two or more things. In general graphs contain x-axis and y axis. Here we deal with a straight line equation.
We need to convert the straight line into slope intercept form so that by calculating we find the slope and intercepts