
How do you graph using slope and intercept of
Answer
468.6k+ views
Hint: In this question we have to plot a graph using slope and intercept of a given straight line. Firstly, we will convert the given equation into a slope intercept form of a straight line. It can be done by first subtracting
Complete step by step answer:
Given the equation of a straight line
We are asked to draw the graph using the slope and intercept of the given line.
So firstly we will try to find out the slope of a line given in the equation (1).
To find this, we need to convert our given equation into slope intercept form of a straight line.
The general equation of a straight line in slope intercept form is given by,
where
Now we convert the given equation of a line into slop intercept form by rearranging the terms.
Consider the equation of a line given in the equation (1).
Subtracting
Combining the like terms we get,
Now dividing throughout by 2 we get,
Rearranging the above equation we get,
Comparing with the standard slope intercept form given in the equation (2), we get,
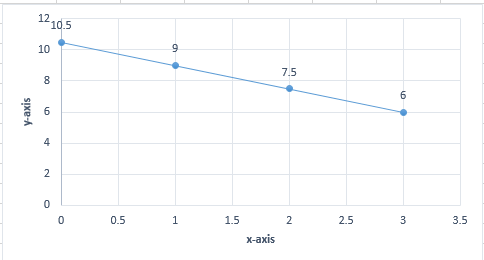
Now to draw a graph of a linear equation, we first assume some values for the variable x and substitute in the above equation and obtain the values of the other variable y.
Then plotting these values of x and y on the x-y plane, we get the graph of the given equation.
We first let different values of x.
Substituting
Substituting
Substituting
Substituting
Note: Graph of a linear equation is always a straight line. Remember the general form of an equation of a straight line given by
Complete step by step answer:
Given the equation of a straight line
We are asked to draw the graph using the slope and intercept of the given line.
So firstly we will try to find out the slope of a line given in the equation (1).
To find this, we need to convert our given equation into slope intercept form of a straight line.
The general equation of a straight line in slope intercept form is given by,
where
Now we convert the given equation of a line into slop intercept form by rearranging the terms.
Consider the equation of a line given in the equation (1).
Subtracting
Combining the like terms we get,
Now dividing throughout by 2 we get,
Rearranging the above equation we get,
Comparing with the standard slope intercept form given in the equation (2), we get,
Now to draw a graph of a linear equation, we first assume some values for the variable x and substitute in the above equation and obtain the values of the other variable y.
Then plotting these values of x and y on the x-y plane, we get the graph of the given equation.
We first let different values of x.
Substituting
Substituting
Substituting
Substituting
| x | 0 | 1 | 2 | 3 |
| y | 10.5 | 9 | 7.5 | 6 |

Note: Graph of a linear equation is always a straight line. Remember the general form of an equation of a straight line given by
Recently Updated Pages
Master Class 11 Accountancy: Engaging Questions & Answers for Success

Master Class 11 Social Science: Engaging Questions & Answers for Success

Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 Physics: Engaging Questions & Answers for Success

Master Class 11 Biology: Engaging Questions & Answers for Success

Class 11 Question and Answer - Your Ultimate Solutions Guide

Trending doubts
Explain why it is said like that Mock drill is use class 11 social science CBSE

The non protein part of an enzyme is a A Prosthetic class 11 biology CBSE

Which of the following blood vessels in the circulatory class 11 biology CBSE

What is a zygomorphic flower Give example class 11 biology CBSE

1 ton equals to A 100 kg B 1000 kg C 10 kg D 10000 class 11 physics CBSE

The deoxygenated blood from the hind limbs of the frog class 11 biology CBSE




