Question

How do you graph using slope and intercept of $2x-3y=7$ ?

Answer 1

Hint: In this question, we have to plot the equation of the curve. Therefore, we have to find the slope and intercept of the equation. Thus, we use the slope-intercept form. As we know that, the slope is the ratio of the vertical change or horizontal change between any two distinct points on the curve. About intercepts, the x-intercept is the point where a line crosses the x-axis, and the y-intercept is the point where a line crosses the y-axis. Thus, we transform the equation into the line of the equation $y=mx+c$ , by subtracting 2x on both sides of the equation, and then multiply both sides by (-1). After that, apply distributive property and do necessary calculations, to get the transformed equation. Thus, we compare the general line of the equation and transformed equation, to get the value of slope and intercepts of the equation. After that, draw the graph of the equation using the slope and intercepts, which is our required answer

Complete step by step answer:
In this question, we have to plot the equation $2x-3y=7$ using slope-intercept form.
As we know, the equation of the line is $y=mx+c$ , where
m is the slope of the equation = $\dfrac{y}{x}=\dfrac{\text{rise}}{\text{run}}$ , means y will go vertically and x will go horizontal
In addition, c is the y-intercept =constant ------------- (1)
Therefore, we rearrange the equation $2x-3y=7$ in the form of $y=mx+c$ , that is
Equation: $2x-3y=7$ ---------- (2)
We will subtract 2x on both sides of the equation (2), we get
$2x-3y-2x=7-2x$
As we know, the same terms will cancel out with opposite signs, we get
$-3y=7-2x$
Now, multiply both sides by (-1) in the above equation, we get
$\Rightarrow (-1).(-3y)=(7-2x).(-1)$
Now, we apply distributive property $(a-b).c=ac-bc$ in the RHS of the above equation, to get
$\begin{align}
  & \Rightarrow 3y=7.(-1)-2x.(-1) \\
 & \Rightarrow 3y=-7+2x \\
\end{align}$
We will divide both sides by 3, to get
$\Rightarrow \dfrac{3}{3}y=-\dfrac{7}{3}+\dfrac{2}{3}x$
Therefore, we get
$\Rightarrow y=-\dfrac{7}{3}+\dfrac{2}{3}x$
$\Rightarrow y=\dfrac{2}{3}x-\dfrac{7}{3}$ ---------- (3)
As we see the above equation has transformed into the equation $y=mx+c$ .
Therefore, on comparing equations (1) and (3), we get that
The slope of the equation $2x-3y=7$ = $m=\dfrac{2}{3}$ , and
The intercept of y-axis $2x-3y=7$ = $c=-\dfrac{7}{3}$ .
So, now we will draw a graph using slope $m=\dfrac{2}{3}$ and y-intercept $c=-\dfrac{7}{3}$ or $c=\left( 0,-\dfrac{7}{3} \right)$ , that is
First, we plot the y-intercept $c=\left( 0,-\dfrac{7}{3} \right)$ of the equation, we get

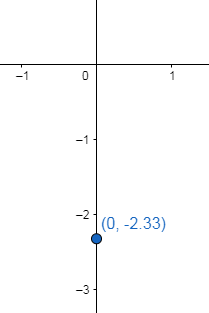
Now, we plot the slope of the equation $m=\dfrac{2}{3}$ , which is we raise 2 units from the y-intercept and then run 3 units, we get

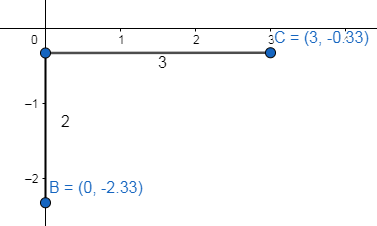
Now, we join points B and C, to get the required line of equation, that is

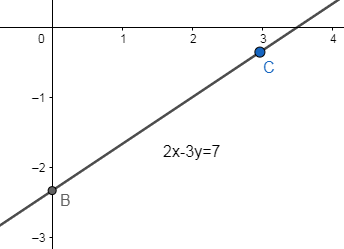
Thus, we draw the graph of equation $2x-3y=7$ with slope $m=\dfrac{2}{3}$ and y-intercept $c=-\dfrac{7}{3}$ or $c=\left( 0,-\dfrac{7}{3} \right)$ .

Note:
Always do proper calculations to get the exact slope and intercept of the equation. Whenever you get fractional intercept, try making them in decimal, it will help you better to draw the graph. You can also find the y-intercept by using the substitution method. Let x=0 in the equation and solve for y, which is the required y-intercept for the answer.