Question

How do you graph the system of inequalities \[x \geqslant 0,y \geqslant 0,x - y > 0\] ?

Answer 1

Hint: Here the given question is to plot the graph for the given set of inequalities, and we have to know that the equation gives the satisfied region as per the relation given in the question, and here we have are provided with three equation hence we need to find the region bounded by these equations together hence a common region will be our required answer.

Complete step-by-step answer:
The given set of equations are \[x \geqslant 0,y \geqslant 0,x - y > 0\]
Here we need to first find the region by each equations and then we will find the common bounded region by all these three equations, hence first we will solve for each equations, on solving we get:
First equation is \[x \geqslant 0\]
This means the area under the positive x axis along with the value of x will be our required region.
Second equation is \[y \geqslant 0\]
This means the area under the positive y axis along with the value of y will be our required region.
Third equation is \[x - y > 0\]
For this equation we need to solve for the values bounded in the curve for which we have to see the region in the graph which will satisfy this equation, on plotting for this curve we get:

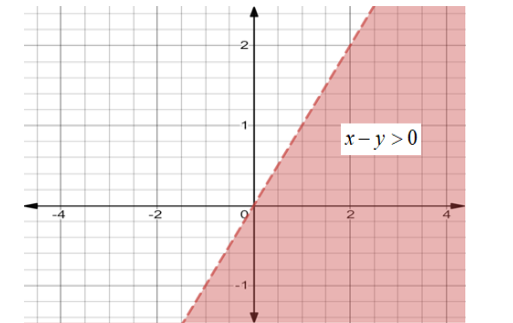
Here we put the value (-1,1) in the equation we get:
 \[
   \Rightarrow x - y > 0 \\
   \Rightarrow - 1 - 1 > 0 \\
   \Rightarrow - 2 > 0 \;
 \]
Here the condition obtained is not possible, hence the upper region is not the required region, the lower region is our required region for this curve.
Now collecting together all the equation region we get:

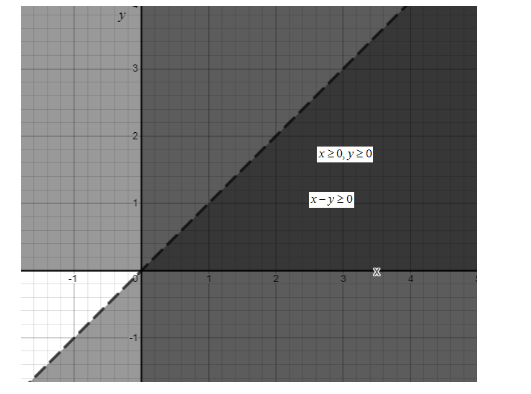
The shaded region is our required answer.

Note: Here for this sort of equations, we need to find solve the linear equation in order to find the valid region, which we can get by putting any coordinates from both side of the curve, and the coordinate which will satisfy the equation, that region would be our required region.