Question

How do you graph the parabola \[y = {x^2} - 3x + 8\] using vertex, intercepts and additional points?

Answer 1

Hint:We compare the given quadratic equation with the general quadratic equation and write values of coefficients. Use the formula to calculate the value of vertex and substitute the values in it. Calculate coordinates of points to plot the graph by substituting different values of x.
* The general quadratic equation is \[a{x^2} + bx + c = 0\]
* Vertex \[(h,k)\]is given by the formula \[h = - \dfrac{b}{{2a}};k = f(h)\], where f is the function given to us.
* For a general quadratic equation \[a{x^2} + bx + c = 0\], roots are given by formula \[x = \dfrac{{ - b \pm \sqrt {{b^2} - 4ac} }}{{2a}}\]

Complete step by step answer:We are given the equation \[y = {x^2} - 3x + 8\]
We compare the equation on right hand side to the general quadratic equation \[a{x^2} + bx + c = 0\]
We get the values \[a = 1,b = - 3,c = 8\]
We know that vertex \[(h,k)\]is given by the formula \[h = - \dfrac{b}{{2a}};k = f(h)\], where f is the function given to us
Here function is \[y = {x^2} - 3x + 8\] … (1)
We substitute the values of ‘a’ and ‘b’ in formula of ‘h’
\[ \Rightarrow h = - \dfrac{{ - ( - 3)}}{{2 \times 1}}\]
\[ \Rightarrow h = \dfrac{3}{2}\]
Now we calculate the value of ‘k’ by substituting value of ‘h’ in place of ‘x’ in the function
\[ \Rightarrow k = f(\dfrac{3}{2})\]
\[ \Rightarrow k = {(\dfrac{3}{2})^2} - 3(\dfrac{3}{2}) + 8\]
\[ \Rightarrow k = \dfrac{9}{4} - \dfrac{9}{2} + 8\]
Take LCM in right hand side of the equation
\[ \Rightarrow k = \dfrac{{9 - 18 + 32}}{4}\]
\[ \Rightarrow k = \dfrac{{23}}{4}\]
So, the vertex \[(h,k) = \left( {\dfrac{3}{2},\dfrac{{23}}{4}} \right)\]
\[\therefore \]The vertex of \[y = {x^2} - 3x + 8\] is \[\left( {\dfrac{3}{2},\dfrac{{23}}{4}} \right)\] … (1)
Now we calculate x and y intercepts of the parabola.
We put \[x = 0\]in the equation, then
\[y = {0^2} - 3 \times 0 + 8\]i.e. \[y = 8\]
So, the point becomes \[(0,8)\] … (2)
Similarly if we put \[y = 0\], then
\[0 = {x^2} - 3x + 8\]
We can solve for the roots of quadratic equation in the right using determinant formula i.e. \[x = \dfrac{{ - b \pm \sqrt {{b^2} - 4ac} }}{{2a}}\]
\[ \Rightarrow x = \dfrac{{ - ( - 3) \pm \sqrt {{{( - 3)}^2} - 4 \times 1 \times 8} }}{{2 \times 1}}\]
Solving the values in square root
\[ \Rightarrow x = \dfrac{{3 \pm \sqrt {9 - 32} }}{2}\]
\[ \Rightarrow x = \dfrac{{3 \pm \sqrt { - 23} }}{2}\]
Since we know \[\sqrt { - 1} = i\], we can write
\[ \Rightarrow x = \dfrac{{3 \pm \sqrt {23} i}}{2}\]
This gives us our both roots as complex roots. So, we do not have a y-intercept.
Now we put \[x = 1\]in the equation, then \[y = 1 - 3 + 8\]i.e. \[y = 6\]
So, the point becomes \[(1,6)\] … (3)
Now we put \[x = - 1\]in the equation, then \[y = {( - 1)^2} - 3( - 1) + 8\]i.e. \[y = 12\]
So, the point becomes \[( - 1,12)\] … (4)
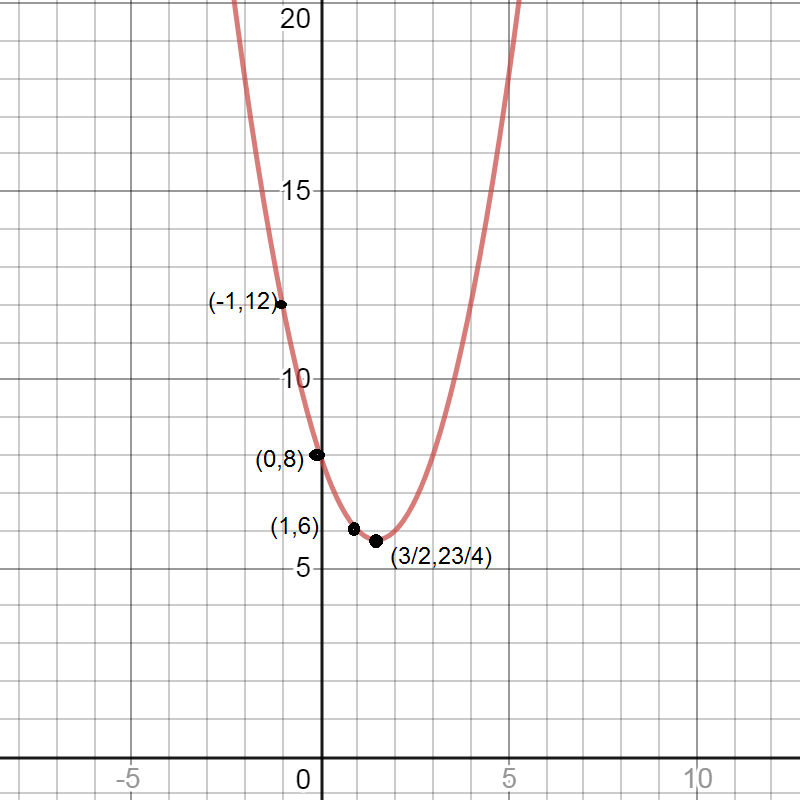
From (!), (2), (3) and (4) and the vertex \[\left( {\dfrac{3}{2},\dfrac{{23}}{4}} \right)\]
We will mark the points\[(0,8)\], \[(1,6)\] and \[( - 1,12)\] on the graph. Also, we know that the equation in the question is equation of parabola as it is similar to general equation of parabola i.e. \[y = a{x^2} + bx + c\]

Note:
Many students make the mistake of writing the coordinates wrong as here y is given in place of \[f(x)\], keep in mind the function is dependent on x and we will write the value of y as the value of the function obtained by putting in the value of x. Also, students should be aware of the fact that whenever they see a quadratic equation, it must be an equation for the parabola so you don’t have to plot all the points.