
How do you graph the parabola \[y = - \dfrac{1}{4}{x^2}\] using vertex intercepts?
Answer
545.4k+ views
Hint: Here in this question, we have to plot the graph of given parabolic equation using the vertex, intercepts and additional points. To find these by comparing the given equation to the vertex form of a quadratic equation \[y = a{\left( {x - h} \right)^2} + k\] where \[\left( {h,k} \right)\] is the vertex of parabola, then the x-intercept is found by putting \[y = 0\;\] in the equation similarly y-intercept is found by putting \[x = 0\] in the equation and the additional points found by giving x values as 0, 1, 2,… to the parabolic equation we get simultaneously the y values.
Complete step-by-step answer:
Consider the equation of parabola
\[y = - \dfrac{1}{4}{x^2}\]
Compare to this equation with the vertex form of a quadratic equation is given by \[y = a{\left( {x - h} \right)^2} + k\] where \[\left( {h,k} \right)\] is the vertex of the parabola. The h represents the horizontal shift and k represents the vertical shift.
Here \[h = 0\], \[k = 0\], \[a = - 1\] Since \[a\] is negative, the parabola opens downward.
Therefore, the vertex of parabola \[V\left( {h,k} \right) = V\left( {0,0} \right)\]it means the parabola initiates at the origin and x intercepts is also at \[\left( {0,0} \right)\]
The Axis of symmetry is \[x = h\] or \[x = 0\].
Since, the parabola is upward & above x-axis hence it wouldn't intersect the x-axis. Now, to find y-intercept we set \[x = 0\]in given equation, as follows i.e.,
\[ \Rightarrow y = - \dfrac{1}{4}{\left( 0 \right)^2}\]
\[ \Rightarrow y = 0\]
Hence, the parabola intersects the y-axis at \[\left( {0,0} \right)\]
Now find the additional points by giving the x values as 0, 1, 2,… to the parabolic equation we get simultaneously the y values.
The additional points are:
The graph of parabola \[y = - \dfrac{1}{4}{x^2}\] is:
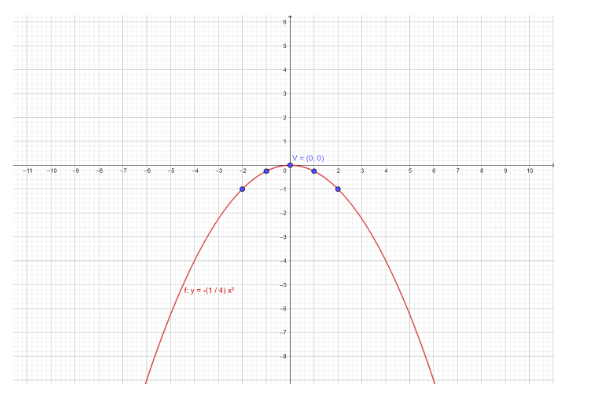
Note: When we see the equation we can easily recognize the kind of graph we can obtain. Usually the equation will be in the form of \[y = a{\left( {x - h} \right)^2} + k\]. Hence by substituting the value of x we can determine the value of y. The graph is plotted x-axis versus y-axis. The graph is of the form 2D.
Complete step-by-step answer:
Consider the equation of parabola
\[y = - \dfrac{1}{4}{x^2}\]
Compare to this equation with the vertex form of a quadratic equation is given by \[y = a{\left( {x - h} \right)^2} + k\] where \[\left( {h,k} \right)\] is the vertex of the parabola. The h represents the horizontal shift and k represents the vertical shift.
Here \[h = 0\], \[k = 0\], \[a = - 1\] Since \[a\] is negative, the parabola opens downward.
Therefore, the vertex of parabola \[V\left( {h,k} \right) = V\left( {0,0} \right)\]it means the parabola initiates at the origin and x intercepts is also at \[\left( {0,0} \right)\]
The Axis of symmetry is \[x = h\] or \[x = 0\].
Since, the parabola is upward & above x-axis hence it wouldn't intersect the x-axis. Now, to find y-intercept we set \[x = 0\]in given equation, as follows i.e.,
\[ \Rightarrow y = - \dfrac{1}{4}{\left( 0 \right)^2}\]
\[ \Rightarrow y = 0\]
Hence, the parabola intersects the y-axis at \[\left( {0,0} \right)\]
Now find the additional points by giving the x values as 0, 1, 2,… to the parabolic equation we get simultaneously the y values.
The additional points are:
| \[x\] | \[ - 2\] | \[ - 1\] | \[0\] | \[1\] | \[2\] |
| \[y = - \dfrac{1}{4}{x^2}\] | \[ - 1\] | \[ - \dfrac{1}{4}\] | \[0\] | \[ - \dfrac{1}{4}\] | \[ - 1\] |
| \[\left( {x,y} \right)\] | \[\left( { - 2, - 1} \right)\] | \[\left( { - 1, - \dfrac{1}{4}} \right)\] | \[\left( {0,0} \right)\] | \[\left( {1, - \dfrac{1}{4}} \right)\] | \[\left( {2, - 1} \right)\] |
The graph of parabola \[y = - \dfrac{1}{4}{x^2}\] is:

Note: When we see the equation we can easily recognize the kind of graph we can obtain. Usually the equation will be in the form of \[y = a{\left( {x - h} \right)^2} + k\]. Hence by substituting the value of x we can determine the value of y. The graph is plotted x-axis versus y-axis. The graph is of the form 2D.
Recently Updated Pages
Master Class 8 Social Science: Engaging Questions & Answers for Success

Master Class 8 English: Engaging Questions & Answers for Success

Class 8 Question and Answer - Your Ultimate Solutions Guide

Master Class 8 Maths: Engaging Questions & Answers for Success

Master Class 8 Science: Engaging Questions & Answers for Success

Master Class 7 English: Engaging Questions & Answers for Success

Trending doubts
What is BLO What is the full form of BLO class 8 social science CBSE

Citizens of India can vote at the age of A 18 years class 8 social science CBSE

Full form of STD, ISD and PCO

Advantages and disadvantages of science

Right to vote is a AFundamental Right BFundamental class 8 social science CBSE

What are the 12 elements of nature class 8 chemistry CBSE





