Question

How do you graph the linear system and estimate the solution: \[y=-x,y=2x+3\]?

Answer 1

Hint: A straight line in the form \[y=mx+c\] has slope m and y-intercept c. We can graph any straight line using any two points lying on it. Two intersecting straight lines meet at a common point which lies on both the lines. A point coordinate can be found based on its distance from each axis.

Complete step by step answer:
As per the given question, we have to graph the given two straight lines and find their intersecting point if they are intersecting lines. The given two straight lines are \[y=-x,y=2x+3\].
We can graph any line based on their intersecting points at x and y axes. For the first line equation \[y=-x\], a point lies on the x-axis when y is zero and it lies on y-axis if x is zero. Since there’s no constant term and slope is -1, the line passes through the origin bisecting the second and fourth quadrants.
For the second line \[y=2x+3\], when \[x=0\], \[y=2x+3=2(0)+3=3\] and when \[y=0\],
\[\Rightarrow y=2x+3\to 0=2x+3\to x=\dfrac{-3}{2}\]. So, \[(0,3)\] and \[(\dfrac{-3}{2},0)\] are the points on the line at y-axis and x-axis respectively.
Here, one line has a negative slope and the other has a positive slope. So, both intersect at a point.
 The following graph shows the two straight lines intersecting each other at a point:
 

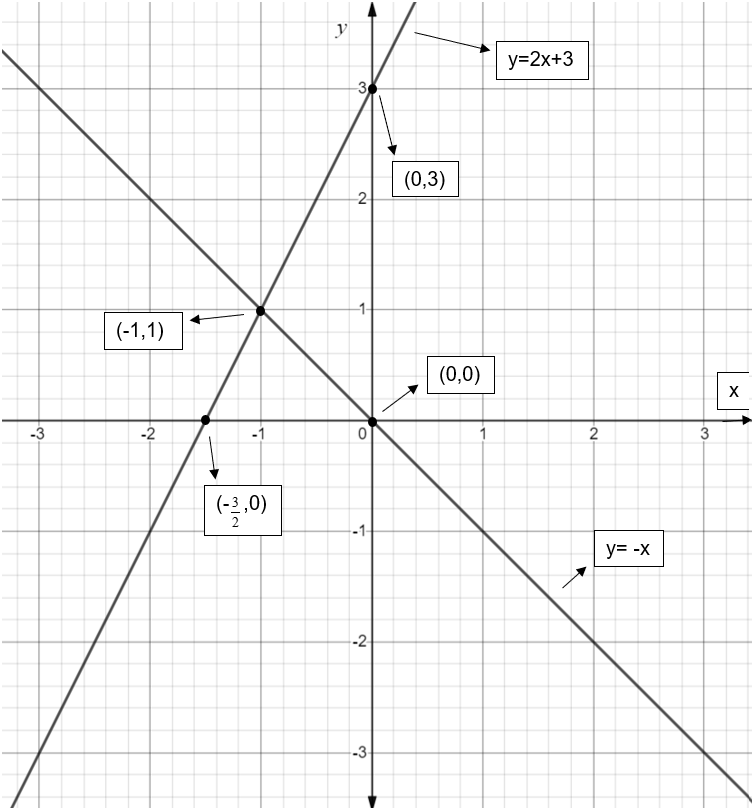
The graph shows the intersection point of the two lines as \[(-1,1)\].

Verification: -
We have the lines \[y=-x\] and \[y=2x+3\]. Substituting equation (1) in equation (2), we get
\[\begin{align}
  & \Rightarrow y=2x+3 \\
 & \Rightarrow -x=2x+3 \\
 & \Rightarrow -x-2x=3 \\
 & \Rightarrow -3x=3 \\
 & \Rightarrow x=-1 \\
\end{align}\]
Substituting \[x=-1\] in the equation (1), we get
\[\begin{align}
  & \Rightarrow y=-x \\
 & \Rightarrow y=-(-1) \\
 & \Rightarrow y=1 \\
\end{align}\]
Hence, verified.

\[\therefore (-1,1)\] is the solution of the lines \[y=-x,y=2x+3\].

Note: In order to solve these types of problems, we need to have knowledge over straight lines and their intersection condition. We should know about how to graph a straight line and to read the intersection point of two intersecting straight lines based on the graph. We should avoid calculation mistakes to get the correct solution.