Question

How do you graph the line $y=\dfrac{4}{5}x+3$ ?

Answer 1

Hint: At first, we compare the given equation with the slope-intercept form of a straight line and find out the slope and y-intercept. Then we plot the point which is the point of intersection of the given line and the $y-axis$ , which is $\left( 0,3 \right)$ and draw another line through this point making an angle ${{\tan }^{-1}}\left( \dfrac{4}{5} \right)$ with the $x$ -axis. This is the required line.

Complete step-by-step solution:
The general slope-intercept form of a straight line is
$y=mx+c$
Where, $m$ is the slope of the line and c is its $y$ -intercept.
And the given equation is
$y=\dfrac{4}{5}x+3$
First of all, we recognise that this is a linear equation, so it is an equation of a straight line. Comparing the given equation with that of the general slope-intercept form, we get
$m=\dfrac{4}{5}$ and $c=3$
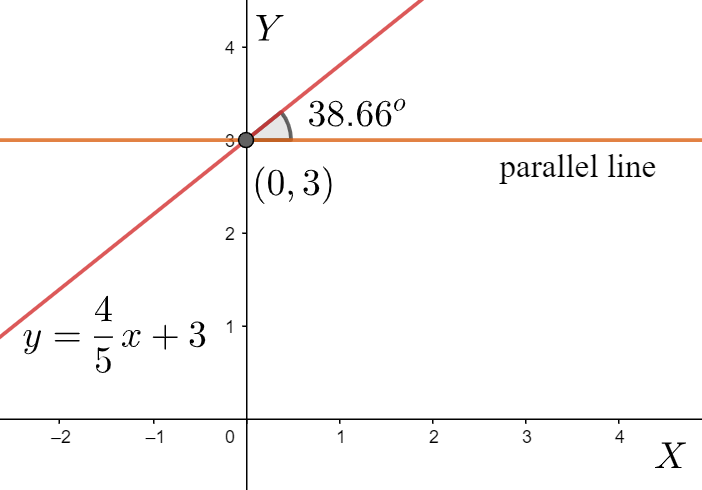
$y$ -intercept $3$ means that the point where the line intersects the $y$ -axis, is $\left( 0,3 \right)$ . Therefore, we plot this point on the graph paper.
Slope of a line means the tangent of the angle that the line makes with the positive $x$ -axis. If we are given the slope, we can find the angle which the line makes by the equation,
$\theta ={{\tan }^{-1}}m$
The angle made by this line with the $x$ -axis then, will be
$\theta ={{\tan }^{-1}}\dfrac{4}{5}$
$\Rightarrow \theta ={{38.66}^{\circ }}$
We draw a line at $\left( 0,3 \right)$ which will be parallel to $x$ -axis. So, the given will make ${{38.66}^{\circ }}$ with the parallel line. With the help of a protractor, we construct this line at $\left( 0,3 \right)$ making ${{38.66}^{\circ }}$ with the parallel line.
Therefore, we can conclude that the last line that we have drawn is nothing but our required line.

Note: Students must be careful while finding out the angle made by the line with the $x$ -axis. They often assume the slope to be the angle and this leads to errors. This problem can also be solved by taking any points that lie on the given line and plot them. Then, if we draw a line joining the points, we get our desired line. This method is a shortcut to the problem.