Question

How do you graph the line $4x + 3y - 12 = 0$?

Answer 1

Hint: Write the given equation in the linear gradient form. Then find the intercepts of x by putting y equal to zero and then intercept y by putting x equal to zero we will get the points of the equation to plot on the graph. Using these points, plot the equation on the graph.

Complete step-by-step solution:
Firstly, we will find the x and y intercepts of the function in order to clearly recognize them. We have to convert the given equation to the linear gradient form that being: $y = mx + c$ …. let it be eq. $\left( 1 \right)$
, where c is the constant determining the y intercept. And m is the gradient of the function.
Therefore, let us do this:
 $4x + 3y - 12 = 0$
Now separate the y variable by taking the x variable and the constant to the RHS of the equation.
$\Rightarrow$$3y = - 4x + 12$
After dividing both side by 3, we get:
$\Rightarrow$ $y = \dfrac{{ - 4x}}{3} + 4$
According to the linear gradient equation $y = mx + c$ we get $m = \dfrac{{ - 4}}{3}$ and $c = 4$ .
This implies that y intercept of the function is 4.
We can also prove this via the statement y intercept where $x = 0$ .
Therefore, $y = 0 \cdot x + 4$
This implies that the y intercept of the function is present at the point A $\left( {0,4} \right)$ .
Similarly, we will do this for x:
Now the linear gradient equation will be of the form $x = my + c$ , where c is the constant determining the x intercept. And m is the gradient of the function.
Therefore, let us do this:
$\Rightarrow$ $4x + 3y - 12 = 0$
Now, separate the x variable by taking the y variable and the constant to the RHS of the equation.
$\Rightarrow$$4x = - 3y + 12$
After dividing both side by 4, we get:
$\Rightarrow$ $x = \dfrac{{ - 3y}}{4} + 3$
According to the linear gradient equation $x = my + c$ we get, $m = \dfrac{{ - 3}}{4}$ and $c = 3$ .
This implies that x intercept of the function is 3.
We can also prove this via the statement x intercept where $y = 0$.
Therefore, $x = 0 \cdot y + 3$
This implies that the y intercept of the function is present at the point B$\left( {3,0} \right)$.
If we plot these points on a Cartesian plane and draw a line between the two points, the graph has been drawn like this:

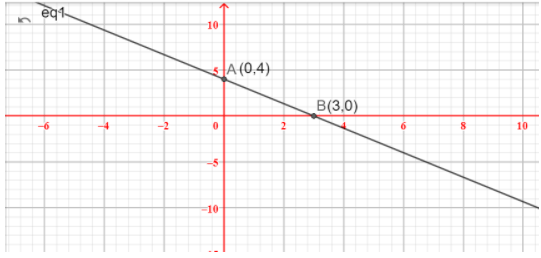
Note: $y = mx + c$ is an important equation. The gradient, m, represents rate of change and the y-intercept, c, represents a starting value.
Any equation that can be rearranged into the form $y = mx + c$ will have a straight line graph. m is the gradient, or steepness of the graph, and c is the y-intercept, or where the line crosses the y-axis.
Gradient is a measure of steepness. As you move along a line from left to right, you might go up, you might go down or you might not change at all.
Gradients can be:
positive – going up
negative – going down
zero - no change (a flat line)