Question

How do you graph the lemniscate ${{r}^{2}}=36\cos 2\theta $?

Answer 1

Hint: We must first convert the given polar equation to the Cartesian equation by using the relations ${{r}^{2}}={{x}^{2}}+{{y}^{2}}$, $x=r\cos \theta $ and $y=r\sin \theta $. Then, we need to check for the symmetry around the coordinate axes. This can be done by replacing $x$ by $-x$ and $y$ by $-y$ in the Cartesian equation. Then on substituting $x=0$, we can find the intersection point with the y axis. Similarly, by substituting $y=0$ we can find the intersection with the x axis. If the curve is found to pass through the origin, then equate the lowest degree term to zero, so as to find out the tangents at the origin.

Complete step-by-step solution:
The polar equation to be graphed is given in the above question as
$\Rightarrow {{r}^{2}}=36\cos 2\theta $
We know that $\cos 2\theta ={{\cos }^{2}}\theta -{{\sin }^{2}}\theta $. Therefore the above equation can be written as
\[\Rightarrow {{r}^{2}}=36\left( {{\cos }^{2}}\theta -{{\sin }^{2}}\theta \right)\]
Multiplying the above equation by ${{r}^{2}}$ we get
\[\begin{align}
  & \Rightarrow {{r}^{4}}=36{{r}^{2}}\left( {{\cos }^{2}}\theta -{{\sin }^{2}}\theta \right) \\
 & \Rightarrow {{r}^{4}}=36\left( {{r}^{2}}{{\cos }^{2}}\theta -{{r}^{2}}{{\sin }^{2}}\theta \right) \\
 & \Rightarrow {{r}^{4}}=36\left( {{\left( r\cos \theta \right)}^{2}}-{{\left( r\sin \theta \right)}^{2}} \right).........\left( i \right) \\
\end{align}\]
Now we know that the polar coordinates are related to the Cartesian coordinates as
$\begin{align}
  & \Rightarrow {{r}^{2}}={{x}^{2}}+{{y}^{2}}........\left( ii \right) \\
 & \Rightarrow x=r\cos \theta ..........\left( iii \right) \\
 & \Rightarrow y=r\sin \theta ..........\left( iv \right) \\
\end{align}$
Substituting the equations (ii), (iii) and (iv) into the equation (i) we get
$\Rightarrow {{\left( {{x}^{2}}+{{y}^{2}} \right)}^{2}}=36\left( {{x}^{2}}-{{y}^{2}} \right)$
Applying the algebraic identity ${{\left( a+b \right)}^{2}}={{a}^{2}}+2ab+{{b}^{2}}$ in the above equation, we can write it as
$\begin{align}
  & \Rightarrow {{\left( {{x}^{2}} \right)}^{2}}+2{{x}^{2}}{{y}^{2}}+{{\left( {{y}^{2}} \right)}^{2}}=36\left( {{x}^{2}}-{{y}^{2}} \right) \\
 & \Rightarrow {{x}^{4}}+2{{x}^{2}}{{y}^{2}}+{{y}^{4}}=36{{x}^{2}}-36{{y}^{2}} \\
 & \Rightarrow {{x}^{4}}+2{{x}^{2}}{{y}^{2}}+{{y}^{4}}-36{{x}^{2}}+36{{y}^{2}}=0.........\left( v \right) \\
\end{align}$
The above equation represents the Cartesian form of the given polar equation. For graphing it, we check the below points.
(i) Symmetry: We can see that the equation (v) contains the even powers of both x and y. Therefore, we can say that the curve will be symmetric with respect to both the x and y axes.
(ii) Intersection with the coordinate axes:
On substituting $x=0$ in the equation (v) we get
$\begin{align}
  & \Rightarrow {{0}^{4}}+2{{\left( 0 \right)}^{2}}{{y}^{2}}+{{y}^{4}}-36{{\left( 0 \right)}^{2}}+36{{y}^{2}}=0 \\
 & \Rightarrow {{y}^{4}}+36{{y}^{2}}=0 \\
 & \Rightarrow {{y}^{2}}\left( {{y}^{2}}+36 \right)=0 \\
 & \Rightarrow {{y}^{2}}=0 \\
 & \Rightarrow y=0 \\
\end{align}$
Since on substituting $x=0$ we obtained $y=0$, the curve must pass through the origin.
On substituting $y=0$ in the equation (v) we get
$\begin{align}
  & \Rightarrow {{x}^{4}}+2{{x}^{2}}{{\left( 0 \right)}^{2}}+{{\left( 0 \right)}^{4}}-36{{x}^{2}}+36{{\left( 0 \right)}^{2}}=0 \\
 & \Rightarrow {{x}^{4}}-36{{x}^{2}}=0 \\
 & \Rightarrow {{x}^{2}}\left( {{x}^{2}}-36 \right)=0 \\
 & \Rightarrow {{x}^{2}}=0,{{x}^{2}}=36 \\
 & \Rightarrow x=0,x=\pm 6 \\
\end{align}$
Therefore, the curve cuts the x axis at $\left( -6,0 \right)$ and $\left( 6,0 \right)$.
(iii) Tangent at origin: For this, we substitute the lowest degree term of equation (v) to zero. From the equation (v) we have
$\begin{align}
  & \Rightarrow {{x}^{4}}+2{{x}^{2}}{{y}^{2}}+{{y}^{4}}-36{{x}^{2}}+36{{y}^{2}}=0 \\
 & \Rightarrow {{x}^{4}}+2{{x}^{2}}{{y}^{2}}+{{y}^{4}}+36\left( {{y}^{2}}-{{x}^{2}} \right)=0 \\
\end{align}$
We can observe that the lowest degree in the above equation is equal to two. Equating the second degree term to zero, we get
$\begin{align}
  & \Rightarrow 36\left( {{y}^{2}}-{{x}^{2}} \right)=0 \\
 & \Rightarrow {{y}^{2}}-{{x}^{2}}=0 \\
 & \Rightarrow {{y}^{2}}={{x}^{2}} \\
 & \Rightarrow y=\pm x \\
\end{align}$
Therefore, the tangents at the origin must be $y=x$ and $y=-x$.
Keeping in mind all of the above three points, we can graph the curve as below.

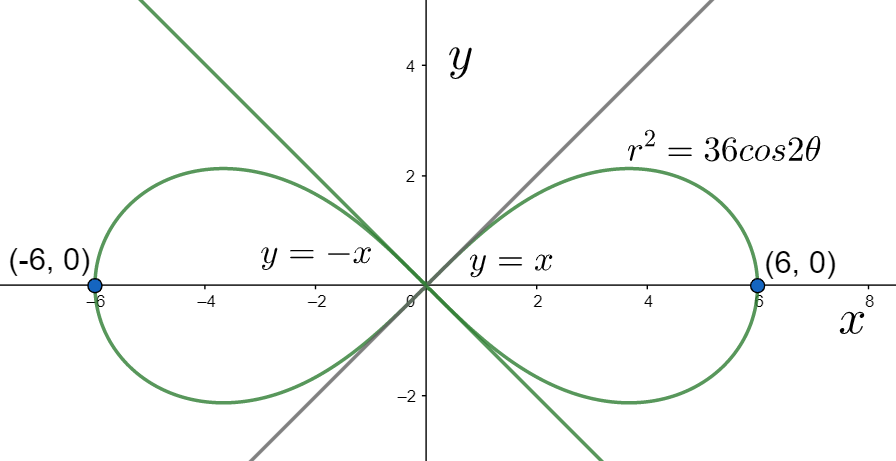
Hence, the given lemniscate has been graphed.

Note: Before finding the tangents at the origin, check whether the curve passes through the origin or not. This is because in the case if the curve does not pass through the origin, the tangent at origin will not exist. We must follow the order of the points as followed in the above solution, that is, symmetry, intersection with coordinate axis, and then tangents at origin.