Question

How do you graph the inequality $ x>-1 $ and $ x<5 $ ?

Answer 1

Hint: The given interval is $ x>-1 $ or $ x<5 $ . The converted equation for variable $ x $ is for $ -1
Complete step-by-step answer:
The given interval of x is $ -1The form $ -1This expression can also be expressed in other ways.
The use of brackets which explains the boundary. The use of ‘ $ \left( {} \right) $ ’ is for open boundary and the use of ‘ $ \left[ {} \right] $ ’ is for closed boundary.
The open boundary is used when we don’t include the boundary point and the closed boundary is used when we include the boundary point.
For our given interval $ x $ can never be equal to -1 or 5. This means we can include neither $ -1 $ nor 5.
The interval will be an open interval. The other expression for $ -1

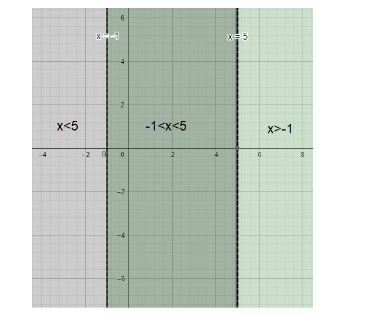
We can also express as the complementary interval where $ x\notin \mathbb{R}\backslash \left( -1,5 \right) $ . This expression is mainly to show where the value of $ x $ can’t be.

Note: The interval is given for a real valued function where the variable does not belong in the imaginary part. That’s why we only used the notation of $ \mathbb{R} $ . Also, in case of imaginary intervals the respective values cannot be compared.