Question

How do you graph the inequality $4x+3y> -12$ ?

Answer 1

Hint: We are given a equation as $4x+3y>-12$ , we have to graph it, to do so we learn about the type of inequality then we will first plot the equality $4x+3y=-12$ on the graph by finding the coordinate that may satisfies the equation. After that we will learn how to choose which side is to be shaded for different kinds of inequality, once we learn that we will mark our shaded part, we will also learn that as inequality is strict the line of equality is marked with a dashed line.

Complete step by step solution:
We are given $4x+3y>-12$ , we can see that is not equality as in place $'='$ we have $'>'$ as we can also see that it has ‘2’ variable ‘x’ and ‘y’ both of which are linear . So our equation is linear inequality in 2 variables.
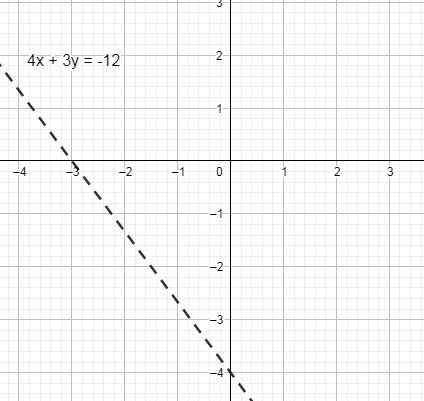
We are asked to graph it, to do so we will first plot the graph of equality $4x+3y=-12$ .
To do so, we find a coordinate that satisfies the above equation.
We get the intercept, so –
At $x=0$ , we have $y=-4$ which satisfies $4x+3y=-12$ .
And we have that –
At $y=0$ we have $x=-3$ which satisfies $4x+3y=-12$ hence we get –
$\left( x,y \right)=\left( 0,-4 \right)=\left( -3,0 \right)$ .
Now, we can see that in our given equality there is strict inequality $\left( > \right)$ so the line which one is going to draw is not part of the solution. So, it will be mark by dashed line $\left( -- \right)$
So, we get the equation –

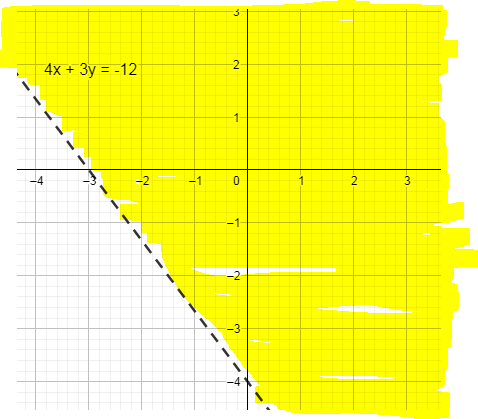
Now we will look for the inequality, to find the required inequality we put $x=0,y=0$ in given inequality, if this point satisfies the inequality then the region toward $\left( 0,0 \right)$ origin is the required inequality.
If not then the region on the opposite is 0 in the required region.
So, we put $x=0,y=0$ in $4x+3y>-12$ .
We get –
$\begin{align}
  & 0+0>-12 \\
 & 0>-12 \\
\end{align}$
It is true.
So, the region toward origin is the correct region.
So, our graph become -

Note: Remember that it is not like that $t>1$ this inequality will get shaded toward origin and $'<'$ is shaded away, in each inequality we need to sketch by first checking the point.
Remember that if the line is passing through equation the we cannot check the region using $\left( 0,0 \right)$ we will then need another point that is lie on right or left of the line, if the point is satisfies the equation we shaded toward point and if not satisfied we shade away from it (opposite of it).