Question

How do you graph the given function $y=3\cos 2\pi x$ and include two full periods?

Answer 1

Hint: We start solving the problem by finding the period of the given function by using the fact that the period of the function $a\cos bx$ is defined as $\dfrac{2\pi }{\left| b \right|}$. We then find the range of the given function by using the fact that the range of the function $a\cos bx$ lies in the interval $\left[ -a,a \right]$. We then find the values of x at which we get maximum, minimum and 0. We then plot these points to get the required graph of the given function.

Complete step by step answer:
According to the problem, we are asked to graph the given function $y=3\cos 2\pi x$ by including two full periods.
We have given the function $y=3\cos 2\pi x$ ---(1).
Let us first find the period of the given function. We know that the period of the function $a\cos bx$ is defined as $\dfrac{2\pi }{\left| b \right|}$. Let us use this result in equation (1).
So, we get the period of the function $y=3\cos 2\pi x$ as $\dfrac{2\pi }{2\pi }=1$.
Now, we need to plot the given function $y=3\cos 2\pi x$ for two full periods, which is $\left[ 0,2 \right]$.
We know that the range of the function $a\cos bx$ lies in the interval $\left[ -a,a \right]$. So, the range of the given function $y=3\cos 2\pi x$ is $\left[ -3,3 \right]$.
We know that the maximum value of $a\cos bx$ occurs at $bx=2n\pi $, $n\in Z$. So, the maximum value of $y=3\cos 2\pi x$ i.e., $y=3$ occurs at $2\pi x=2n\pi \Leftrightarrow x=n$, $n\in Z$ ---(1).
We know that the minimum value of $a\cos bx$ occurs at $bx=\left( 2n+1 \right)\pi $, $n\in Z$. So, the maximum value of $y=3\cos 2\pi x$ i.e., $y=-3$ occurs at $2\pi x=\left( 2n+1 \right)\pi \Leftrightarrow x=n+\dfrac{1}{2}$, $n\in Z$ ---(2).
We know that the $a\cos bx=0$ occurs at $bx=\left( 2n+1 \right)\dfrac{\pi }{2}$, $n\in Z$. So, the maximum value of $y=3\cos 2\pi x$ i.e., $y=0$ occurs at $2\pi x=\left( 2n+1 \right)\dfrac{\pi }{2}\Leftrightarrow x=\dfrac{2n+1}{4}$, $n\in Z$ ---(3).
Now, let us plot the given function by using the results obtained from equations (1), (2) and (3).

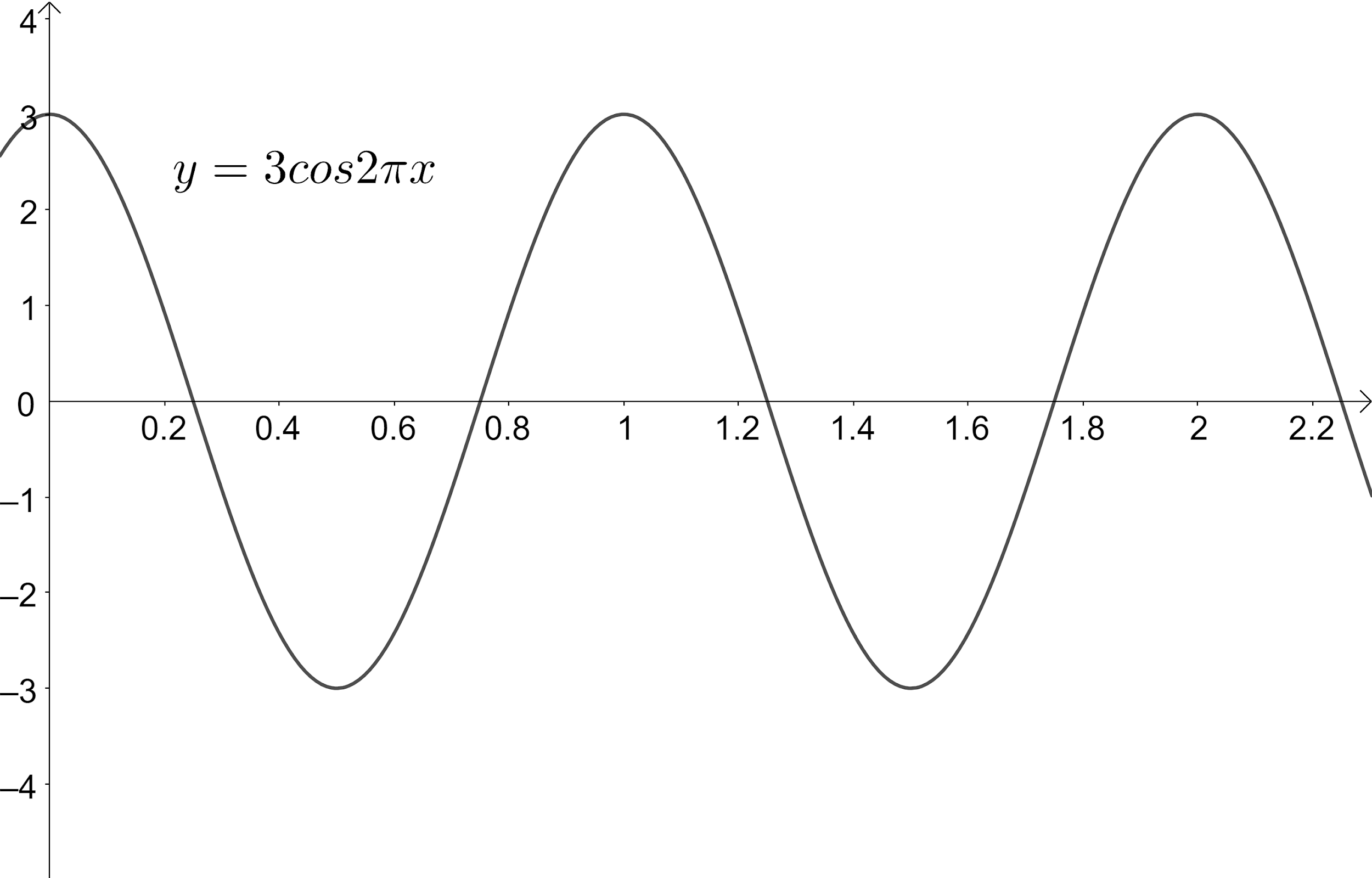
Note:
We should not confuse while finding the general solution for the maximum, minimum values of the given function. We should keep in mind that the period will always be greater than 0 while solving this type of problem. We should not make calculation mistakes while solving this type of problem. Similarly, we can expect problems graphing the given function $y=\tan 2\pi x$ and include four full periods.