
Graph the following equation $ y = 2{x^2} + 12x + 16 $
Answer
544.5k+ views
Hint: In this problem, we have to graph the following equation $ y = 2{x^2} + 12x + 16 $ and this equation is similar to the general equation of parabola i.e, $ y = a{x^2} + bx + c $ . A plane curve that is almost u-shaped or we can say is of a bowl shaped and symmetrical in nature is called a parabola.
Formula Used: The formula of the axis of symmetry(x) is,
$ x = \dfrac{{ - b}}{{2a}} $
Where, b and a is used from the general equation of parabola i.e, $ y = a{x^2} + bx + c $ .
Complete step by step solution:
Firstly, we will compare the general equation of the parabola and the equation given in the question. On comparing, we get,
$ \Rightarrow a = 2,b = 12,c = 16 $
Secondly, we need to find the axis of symmetry by the formula given above.
$
\Rightarrow x = \dfrac{{ - 12}}{{2 \times 2}} \\
\Rightarrow x = \dfrac{{ - 12}}{4} \\
\Rightarrow x = - 3 \;
$
Now, $ - 3 $ is the axis of symmetry and now, we will find the value of the vertex and it is found, when we substitute the value of (x) axis of symmetry in the equation given in the question.
$
\Rightarrow y = 2{\left( { - 3} \right)^2} + 12\left( { - 3} \right) + 16 \\
\Rightarrow y = 2\left( 9 \right) + 12 \times \left( { - 3} \right) + 16 \\
\Rightarrow y = 2 \times 9 - 36 + 16 \\
\Rightarrow y = 18 - 20 \\
\Rightarrow y = - 2 \;
$
Now, $ - 2 $ is the vertex and now we have our first point to locate on the graph i.e, $ \left( { - 3, - 2} \right) $ .
Now, to find the other coordinates, different values of x are placed in the equation and then the values of y are computed and then, we will form a table of values through which we can plot a graph.
For example, if the value of x is $ - 5 $ , then, the value of y is $ 6 $ .
$
\Rightarrow y = 2{\left( { - 5} \right)^2} + 12\left( { - 5} \right) + 16 \\
\Rightarrow y = 2 \times 25 + 12 \times \left( { - 5} \right) + 16 \\
\Rightarrow y = 50 - 60 + 16 \\
\Rightarrow y = - 10 + 16 \\
\Rightarrow y = 6 \;
$
Now, we will form a table for the values of x and y.
Hence, the graph formed by these points is,
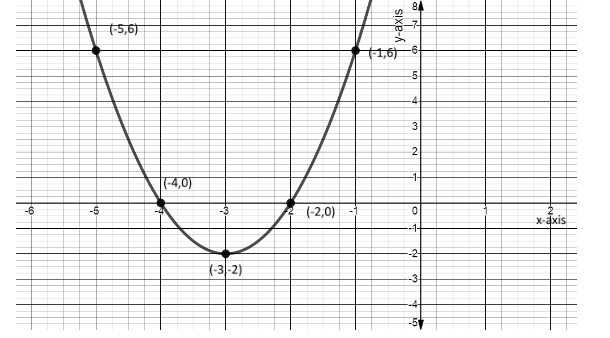
Note: To make the graph of the following equation $ y = 2{x^2} + 12x + 16 $ , firstly, we need to find the axis of symmetry and the vertex and after that we will assume the values of x and substitute in the equation to find the value of y, and after finding the values we will locate these points on the graph.
Formula Used: The formula of the axis of symmetry(x) is,
$ x = \dfrac{{ - b}}{{2a}} $
Where, b and a is used from the general equation of parabola i.e, $ y = a{x^2} + bx + c $ .
Complete step by step solution:
Firstly, we will compare the general equation of the parabola and the equation given in the question. On comparing, we get,
$ \Rightarrow a = 2,b = 12,c = 16 $
Secondly, we need to find the axis of symmetry by the formula given above.
$
\Rightarrow x = \dfrac{{ - 12}}{{2 \times 2}} \\
\Rightarrow x = \dfrac{{ - 12}}{4} \\
\Rightarrow x = - 3 \;
$
Now, $ - 3 $ is the axis of symmetry and now, we will find the value of the vertex and it is found, when we substitute the value of (x) axis of symmetry in the equation given in the question.
$
\Rightarrow y = 2{\left( { - 3} \right)^2} + 12\left( { - 3} \right) + 16 \\
\Rightarrow y = 2\left( 9 \right) + 12 \times \left( { - 3} \right) + 16 \\
\Rightarrow y = 2 \times 9 - 36 + 16 \\
\Rightarrow y = 18 - 20 \\
\Rightarrow y = - 2 \;
$
Now, $ - 2 $ is the vertex and now we have our first point to locate on the graph i.e, $ \left( { - 3, - 2} \right) $ .
Now, to find the other coordinates, different values of x are placed in the equation and then the values of y are computed and then, we will form a table of values through which we can plot a graph.
For example, if the value of x is $ - 5 $ , then, the value of y is $ 6 $ .
$
\Rightarrow y = 2{\left( { - 5} \right)^2} + 12\left( { - 5} \right) + 16 \\
\Rightarrow y = 2 \times 25 + 12 \times \left( { - 5} \right) + 16 \\
\Rightarrow y = 50 - 60 + 16 \\
\Rightarrow y = - 10 + 16 \\
\Rightarrow y = 6 \;
$
Now, we will form a table for the values of x and y.
| Value of x | Value of y |
| $ - 5 $ | $ 6 $ |
| $ - 4 $ | $ 0 $ |
| $ - 3 $ | $ - 2 $ |
| $ - 2 $ | $ 0 $ |
| $ - 1 $ | $ 6 $ |
Hence, the graph formed by these points is,

Note: To make the graph of the following equation $ y = 2{x^2} + 12x + 16 $ , firstly, we need to find the axis of symmetry and the vertex and after that we will assume the values of x and substitute in the equation to find the value of y, and after finding the values we will locate these points on the graph.
Recently Updated Pages
Master Class 8 Social Science: Engaging Questions & Answers for Success

Master Class 8 English: Engaging Questions & Answers for Success

Class 8 Question and Answer - Your Ultimate Solutions Guide

Master Class 8 Maths: Engaging Questions & Answers for Success

Master Class 8 Science: Engaging Questions & Answers for Success

Master Class 7 English: Engaging Questions & Answers for Success

Trending doubts
Difference Between Plant Cell and Animal Cell

Fill the blanks with the suitable prepositions 1 The class 9 english CBSE

Who is eligible for RTE class 9 social science CBSE

Which places in India experience sunrise first and class 9 social science CBSE

What is pollution? How many types of pollution? Define it

Name 10 Living and Non living things class 9 biology CBSE




