Question

How do you graph the equation $y=-\dfrac{1}{5}x+2$ ?

Answer 1

Hint: First of all, put the x coordinate of this line as 0 and then see what value of y coordinate you are getting and plot that point on the graph paper. After that, put y coordinate as 0 in the given straight line and then see what is the x coordinate corresponding to this y coordinate and then plot this coordinate on the graph paper. Now, join these two points. Joining these two points will give you a straight line.

Complete step by step answer:
The equation of a straight line given in the above problem is as follows:
$y=-\dfrac{1}{5}x+2$………… Eq. (1)
We are asked to draw the above straight line on the graph paper. For that, we are going to substitute x coordinate as 0 in the above straight line and then solve the remaining equation to get the y coordinate.
$\begin{align}
  & y=-\dfrac{1}{5}\left( 0 \right)+2 \\
 & \Rightarrow y=0+2 \\
 & \Rightarrow y=2 \\
\end{align}$
From the above we got the one point i.e. $\left( 0,2 \right)$. Let us name this point as A. Now, we are going to plot this point A (0,2) on the graph paper.

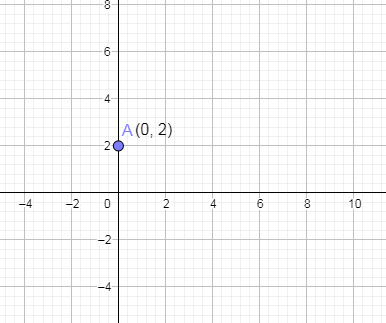
Now, we are going to put the y coordinate as 0 in eq. (1) and solve the remaining equation to get the value of x.
$0=-\dfrac{1}{5}x+2$
Subtracting 2 on both the sides we get,
$\begin{align}
  & 0-2=-\dfrac{1}{5}x+2-2 \\
 & \Rightarrow -2=-\dfrac{1}{5}x \\
\end{align}$
Negative signs from both the sides will be cancelled out and then we cross multiply the above equation.
$\begin{align}
  & \Rightarrow 2\left( 5 \right)=x \\
 & \Rightarrow 10=x \\
\end{align}$
From the above, we got the second coordinate as $\left( 10,0 \right)$. Now, let us name this point as B and plot this point B on the graph paper.

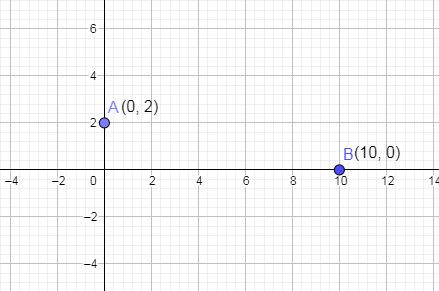
Now, we are going to join the points A and B to draw a straight line.

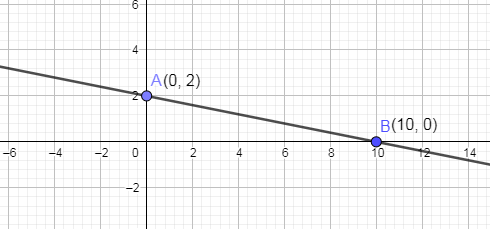
Hence, we have plotted the straight line $y=-\dfrac{1}{5}x+2$ on the graph paper.

Note: You can check that the graph that you have plotted is correct or not. Let us mark the x coordinate as 5 on the straight line and then draw a perpendicular on the y axis from this point and see the point on the y axis on which the foot of the perpendicular is lying.

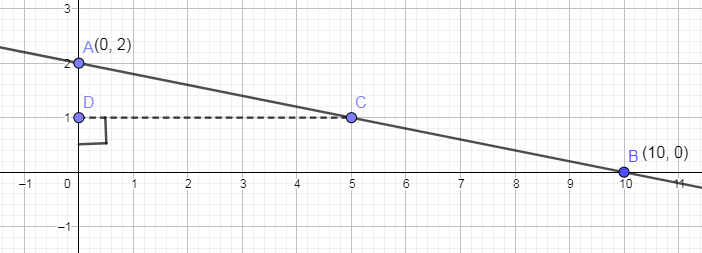
In the above graph C is the point where x coordinate is 5 and the foot of the perpendicular from C is D and coordinate of y of point D is 1.
Now, let us substitute x as 5 in eq. (1) and see the value of y from the equation.
$\begin{align}
  & y=-\dfrac{1}{5}\left( 5 \right)+2 \\
 & \Rightarrow y=-1+2 \\
 & \Rightarrow y=1 \\
\end{align}$
As you can see that we are getting the same value of y coordinate that we were getting from the graph so this shows that the graph which we have plotted is correct.