
How do you graph the equation $y=8x$ by making a table and what is its domain and range?
Answer
545.4k+ views
Hint: We recall domain, range and graph of a function. We take five inputs $x=-2,-1,0,1,2$ to and find the corresponding outputs $y$ to make the table. We join the points $\left( x,y \right)$ to get the graph. We see if there are any points where we cannot find output and exclude it to get the domain. We find the collections of outputs to find the range.
Complete step by step solution:
We know that the domain a function $f$ is the set where it takes inputs and range co-domain is the set where it maps the inputs outputs. The set of outputs is called range. If $x$ is the variable which assigns the inputs and $y$ is the variable which assigned to outputs then we have
\[y=f\left( x \right)\]
We also know that the set of collection of points $\left( x,y \right)=\left( x,f\left( x \right) \right)$ is called graph of the function $f$ and the locus traced by such points is called curve of $f$. We are given in the question the following equation
\[y=8x\]
So the function is $f\left( x \right)=8x$. We take points from the real number set $x=-2,-1,0,1,2$ and find the corresponding outputs $y$ and the points $\left( x,y \right)$ in table.
We plot the above obtained points and join them to get the curve for $y=8x$. \[\]
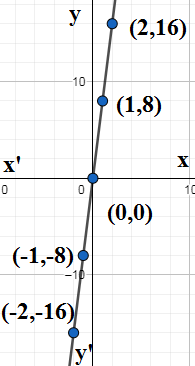
We see that for every real number $x$ we get a real number $y$ which 8 times $x$. So $f\left( x \right)=8x$ can take very real number as input and hence the domain of $f\left( x \right)$ is real number set $\mathsf{\mathbb{R}}$.We know that multiplication is closed under real number set . Since both 8 and $x$ are real numbers $8x$ is real number and hence all the outputs are real numbers. So the range of $f\left( x \right)$ is also $\mathsf{\mathbb{R}}$.
Note: We note that the line passing through the origin has the equation $y=mx$ where $m$ is the slope of the equation like the given equation $y=8x$. We also note that if for every $y$ in the range there exist only $x$ in the domain then we can define as inverse function ${{f}^{-1}}\left( x \right)$ as ${{f}^{-1}}\left( y \right)=x$. Here the inverse of $f\left( x \right)=8x$ is ${{f}^{-1}}\left( x \right)=\dfrac{1}{8}x$. We note that curves of $f,{{f}^{-1}}$ are reflections of each other about the line $y=x$.
Complete step by step solution:
We know that the domain a function $f$ is the set where it takes inputs and range co-domain is the set where it maps the inputs outputs. The set of outputs is called range. If $x$ is the variable which assigns the inputs and $y$ is the variable which assigned to outputs then we have
\[y=f\left( x \right)\]
We also know that the set of collection of points $\left( x,y \right)=\left( x,f\left( x \right) \right)$ is called graph of the function $f$ and the locus traced by such points is called curve of $f$. We are given in the question the following equation
\[y=8x\]
So the function is $f\left( x \right)=8x$. We take points from the real number set $x=-2,-1,0,1,2$ and find the corresponding outputs $y$ and the points $\left( x,y \right)$ in table.
| $x$ | $y=8x$ | $\left( x,y \right)$ |
| $-2$ | $8\times \left( -2 \right)=-16$ | $\left( -2,-16 \right)$ |
| $-1$ | $8\times \left( -1 \right)=8$ | $\left( -1,-8 \right)$ |
| 0 | $8\times 0=0$ | $\left( 0,0 \right)$ |
| 1 | $8\times 1=8$ | $\left( 1,8 \right)$ |
| 2 | $8\times 2=16$ | $\left( 2,16 \right)$ |
We plot the above obtained points and join them to get the curve for $y=8x$. \[\]

We see that for every real number $x$ we get a real number $y$ which 8 times $x$. So $f\left( x \right)=8x$ can take very real number as input and hence the domain of $f\left( x \right)$ is real number set $\mathsf{\mathbb{R}}$.We know that multiplication is closed under real number set . Since both 8 and $x$ are real numbers $8x$ is real number and hence all the outputs are real numbers. So the range of $f\left( x \right)$ is also $\mathsf{\mathbb{R}}$.
Note: We note that the line passing through the origin has the equation $y=mx$ where $m$ is the slope of the equation like the given equation $y=8x$. We also note that if for every $y$ in the range there exist only $x$ in the domain then we can define as inverse function ${{f}^{-1}}\left( x \right)$ as ${{f}^{-1}}\left( y \right)=x$. Here the inverse of $f\left( x \right)=8x$ is ${{f}^{-1}}\left( x \right)=\dfrac{1}{8}x$. We note that curves of $f,{{f}^{-1}}$ are reflections of each other about the line $y=x$.
Recently Updated Pages
Basicity of sulphurous acid and sulphuric acid are

Master Class 12 Business Studies: Engaging Questions & Answers for Success

Master Class 12 Economics: Engaging Questions & Answers for Success

Master Class 12 English: Engaging Questions & Answers for Success

Master Class 12 Maths: Engaging Questions & Answers for Success

Master Class 12 Social Science: Engaging Questions & Answers for Success

Trending doubts
What are the major means of transport Explain each class 12 social science CBSE

Which are the Top 10 Largest Countries of the World?

Draw a labelled sketch of the human eye class 12 physics CBSE

How much time does it take to bleed after eating p class 12 biology CBSE

Explain sex determination in humans with line diag class 12 biology CBSE

Differentiate between homogeneous and heterogeneous class 12 chemistry CBSE




