Question

How do you graph the equation \[y - 2 = 3\left( {x - 1} \right)\] ?

Answer 1

Hint: Here, the given equation is an equation of the straight line. We will first write it in slope in the slope-intercept form and compare it by general slope-intercept form. So from there, we will get the value of the slope of the line and then the \[y\] intercept. Then we will find the value of the \[x\] intercepts by putting the value of \[y\] as zero. Then using the slope and the intercepts, we will draw the graph accordingly.

Complete step by step solution:
Here we need to find the graph for the given equation and the given equation is \[y - 2 = 3\left( {x - 1} \right)\].
Now, we will write it in standard form. We will use the distributive property in the right-hand side expression.
\[ \Rightarrow y - 2 = 3x - 3\]
Now, we will add 2 on both sides. Therefore, we get
\[\begin{array}{l} \Rightarrow y - 2 + 2 = 3x - 3 + 2\\ \Rightarrow y = 3x - 1\end{array}\]
We know that this is an equation of straight line and the given equation is written in the slope intercept form.
We know that the slope-intercept form of an equation is given by\[y = mx + b\], where \[m\] is the slope of the line and \[b\] is the \[y\] intercept.
Now, we will compare this equation with the given equation.
Slope in this case is \[3\] and \[y\] intercept is equal to \[ - 1\].
Now, we will find the \[x\] intercepts by putting the value of \[y\] as zero in \[y = 3x - 1\]. Therefore, we get
\[0 = 3x - 1\]
Now, adding 1 on both sides, we get
\[ \Rightarrow 0 + 1 = 3x - 1 + 1\]
\[ \Rightarrow 1 = 3x\]
Now, dividing both sides by 3, we get
\[ \Rightarrow \dfrac{1}{3} = \dfrac{{3x}}{3}\]
On further simplification, we get
\[\begin{array}{l} \Rightarrow \dfrac{1}{3} = x\\ \Rightarrow x = \dfrac{1}{3}\end{array}\]
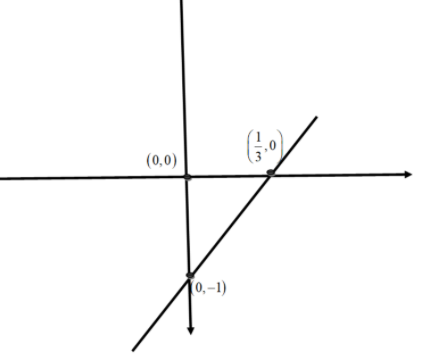
Therefore, the \[x\] intercept is equal to \[\dfrac{1}{3}\].
Now, we will draw the graph using the slope and the intercepts.

Note:
A coordinate plane is a two-dimensional number line where the vertical line is called the \[y\]-axis and the horizontal is called the \[x\]-axis. These lines are perpendicular and intersect at their zero points. Their intersection point is called the origin and usually denoted as \[O\].
The slope of a line is defined as the value which measures the steepness of the line or the inclination of the line with the \[x\] axis. A slope of any line can either be a positive number, negative number, zero, or undefined. As we have discussed, the slope of a vertical line that is parallel to the \[y\] axis is undefined. Similarly, the slope of a horizontal line that is parallel to the axis is zero.