
How do you graph the equation $ - 4x + 2y = 8$?
Answer
561k+ views
Hint: Plotting a graph depends on the type of equation we have. A linear equation will always give a straight line, while a quadratic equation gives a parabolic shape. In the problem we have a linear equation, so we will get a straight line in the graph. For drawing a straight line, we need to have at least two points that satisfy the given linear equation. For finding the two points which satisfy the given line we need to take two points in the coordinate system like $\left( {a,0} \right)$ and $\left( {0,b} \right)$. Now we will substitute the points in the given equation and calculate the values of $a$ and $b$. Then take a minimum of 5 points and plot the points. After plotting the points, join the points with a smooth freehand curve and identify the curve that we have obtained.
Complete step-by-step solution:
We know that the graph of a function is the locus of points $\left( {x,y} \right)$ such that $y = f\left( x \right)$ where x, y are real numbers. We are given the following quadratic polynomial function,
$ \Rightarrow - 4x + 2y = 8$
So, let us put $y = 0$ and find the x-intercept. We have,
$ \Rightarrow - 4x + 2 \times 0 = 8$
Simplify the terms,
$ \Rightarrow - 4x = 8$
Divide both sides by -4,
$ \Rightarrow x = - 2$
It means the curve cuts the x-axis at $\left( { - 2,0} \right)$.
Let us put $x = 0$ and find the y-intercept. We have,
$ \Rightarrow - 4 \times 0 + 2y = 8$
Simplify the terms,
$ \Rightarrow 2y = 8$
Divide both sides by 2,
$ \Rightarrow y = 4$
It means the curve cuts the y-axis at $\left( {0,4} \right)$.
We have already two points for the equation $\left( { - 2,0} \right)$ and $\left( {0,4} \right)$. We find y for three more points.
At $x = - 1$ we have,
$ \Rightarrow - 4 \times - 1 + 2y = 8$
Simplify the terms,
$ \Rightarrow 4 + 2y = 8$
Move the constant part on right side,
$ \Rightarrow 2y = 4$
Divide both sides by 2,
$ \Rightarrow y = 2$
At $x = 1$ we have,
$ \Rightarrow - 4 \times 1 + 2y = 8$
Simplify the terms,
$ \Rightarrow - 4 + 2y = 8$
Move the constant part on right side,
$ \Rightarrow 2y = 12$
Divide both sides by 2,
$ \Rightarrow y = 6$
At $x = - 3$ we have,
$ \Rightarrow - 4 \times - 3 + 2y = 8$
Simplify the terms,
$ \Rightarrow 12 + 2y = 8$
Move the constant part on right side,
$ \Rightarrow 2y = - 4$
Divide both sides by 2,
$ \Rightarrow y = - 2$
So, we draw the table for x and y.
We plot the above points and join them to have the graph as
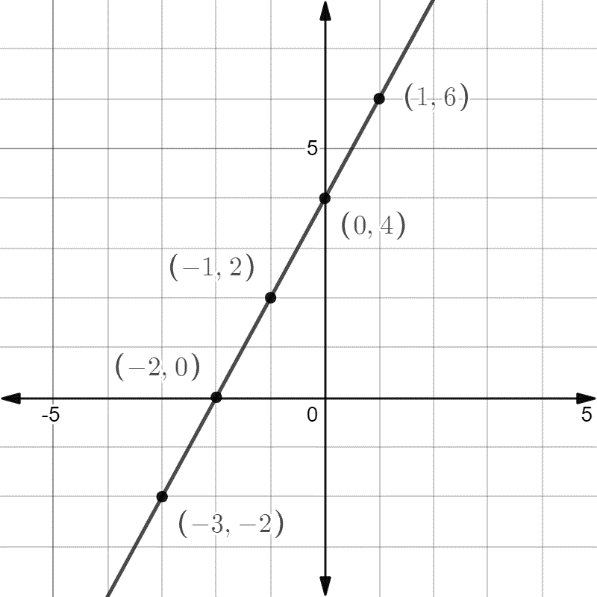
Note: For this type of problem in which a graph of linear equations is required to draw. If the graph of the equation is not coming to a straight line then we can say that the points taken are wrong as the graph of the linear equation is always a straight line. So, if the graph through given points is a straight line and passing through them then it will be a correct sketch for the given linear equation.
Complete step-by-step solution:
We know that the graph of a function is the locus of points $\left( {x,y} \right)$ such that $y = f\left( x \right)$ where x, y are real numbers. We are given the following quadratic polynomial function,
$ \Rightarrow - 4x + 2y = 8$
So, let us put $y = 0$ and find the x-intercept. We have,
$ \Rightarrow - 4x + 2 \times 0 = 8$
Simplify the terms,
$ \Rightarrow - 4x = 8$
Divide both sides by -4,
$ \Rightarrow x = - 2$
It means the curve cuts the x-axis at $\left( { - 2,0} \right)$.
Let us put $x = 0$ and find the y-intercept. We have,
$ \Rightarrow - 4 \times 0 + 2y = 8$
Simplify the terms,
$ \Rightarrow 2y = 8$
Divide both sides by 2,
$ \Rightarrow y = 4$
It means the curve cuts the y-axis at $\left( {0,4} \right)$.
We have already two points for the equation $\left( { - 2,0} \right)$ and $\left( {0,4} \right)$. We find y for three more points.
At $x = - 1$ we have,
$ \Rightarrow - 4 \times - 1 + 2y = 8$
Simplify the terms,
$ \Rightarrow 4 + 2y = 8$
Move the constant part on right side,
$ \Rightarrow 2y = 4$
Divide both sides by 2,
$ \Rightarrow y = 2$
At $x = 1$ we have,
$ \Rightarrow - 4 \times 1 + 2y = 8$
Simplify the terms,
$ \Rightarrow - 4 + 2y = 8$
Move the constant part on right side,
$ \Rightarrow 2y = 12$
Divide both sides by 2,
$ \Rightarrow y = 6$
At $x = - 3$ we have,
$ \Rightarrow - 4 \times - 3 + 2y = 8$
Simplify the terms,
$ \Rightarrow 12 + 2y = 8$
Move the constant part on right side,
$ \Rightarrow 2y = - 4$
Divide both sides by 2,
$ \Rightarrow y = - 2$
So, we draw the table for x and y.
| X | 0 | -2 | -1 | 1 | -3 |
| Y | 4 | 0 | 2 | 6 | -2 |
We plot the above points and join them to have the graph as

Note: For this type of problem in which a graph of linear equations is required to draw. If the graph of the equation is not coming to a straight line then we can say that the points taken are wrong as the graph of the linear equation is always a straight line. So, if the graph through given points is a straight line and passing through them then it will be a correct sketch for the given linear equation.
Recently Updated Pages
Master Class 6 Science: Engaging Questions & Answers for Success

Class 6 Question and Answer - Your Ultimate Solutions Guide

Master Class 6 Social Science: Engaging Questions & Answers for Success

Master Class 5 Science: Engaging Questions & Answers for Success

Class 5 Question and Answer - Your Ultimate Solutions Guide

Master Class 5 English: Engaging Questions & Answers for Success

Trending doubts
What is BLO What is the full form of BLO class 8 social science CBSE

Citizens of India can vote at the age of A 18 years class 8 social science CBSE

Full form of STD, ISD and PCO

Convert 40circ C to Fahrenheit A 104circ F B 107circ class 8 maths CBSE

Advantages and disadvantages of science

Right to vote is a AFundamental Right BFundamental class 8 social science CBSE





